| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | ||
| 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 13 | 14 | 15 | 16 | 17 | 18 | 19 |
| 20 | 21 | 22 | 23 | 24 | 25 | 26 |
| 27 | 28 | 29 | 30 |
- RCNN
- CNN
- nerf
- VIT
- rl
- CS224N
- GaN
- Googlenet
- cv
- 자연어처리
- transformer
- 연세대학교 인공지능학회
- Fast RCNN
- YAI 9기
- NLP #자연어 처리 #CS224N #연세대학교 인공지능학회
- 3D
- PytorchZeroToAll
- NLP
- cl
- GAN #StyleCLIP #YAI 11기 #연세대학교 인공지능학회
- YAI
- Perception 강의
- YAI 10기
- YAI 8기
- 컴퓨터비전
- 강화학습
- Faster RCNN
- 컴퓨터 비전
- YAI 11기
- CS231n
- Today
- Total
연세대 인공지능학회 YAI
[논문 리뷰] Conv-TasNet: Surpassing Ideal Time-Frequency magnitude Masking for Speech Separation 본문
[논문 리뷰] Conv-TasNet: Surpassing Ideal Time-Frequency magnitude Masking for Speech Separation
_YAI_ 2022. 9. 26. 21:20Conv-TasNet: Surpassing Ideal Time-Frequency magnitude Masking for Speech Separation
https://arxiv.org/abs/1809.07454
Conv-TasNet: Surpassing Ideal Time-Frequency Magnitude Masking for Speech Separation
Single-channel, speaker-independent speech separation methods have recently seen great progress. However, the accuracy, latency, and computational cost of such methods remain insufficient. The majority of the previous methods have formulated the separation
arxiv.org
*YAI 10기 이진우님께서 음성팀에서 작성해주신 리뷰입니다.
1. Introduction
Most previous speech separation approaches have been formulated in the time-frequency (T-F) representation of the mixture signal
- estimated from the waveform using short-time Fourier transform (STFT)
- The output (waveform of each source) is calculated using iSTFT.
Drawbacks of T-F masking
- Not necessarily optimal for speech separation
- Then let’s replace the STFT with a data-driven representation
- Erroneous estimation of phase
- Even when the ideal clean magnitude spectrograms are applied to the mixture → imperfect reconstruction
- due to STFT calculation which includes a long temporal windowing
- limits its applicability in real-time, low-latency applicationsLatency problem
- No more decoupling the mag and phase!
- Let’s directly separate in time domain!
Drawbacks of TasNet
- Smaller kernel size == len(wav segments)
- `training of the LSTMs become unmanageable
- Large number of parameters
- increased computational cost
- long temporal dependencies of LSTM
- inconsistent separation accuracy
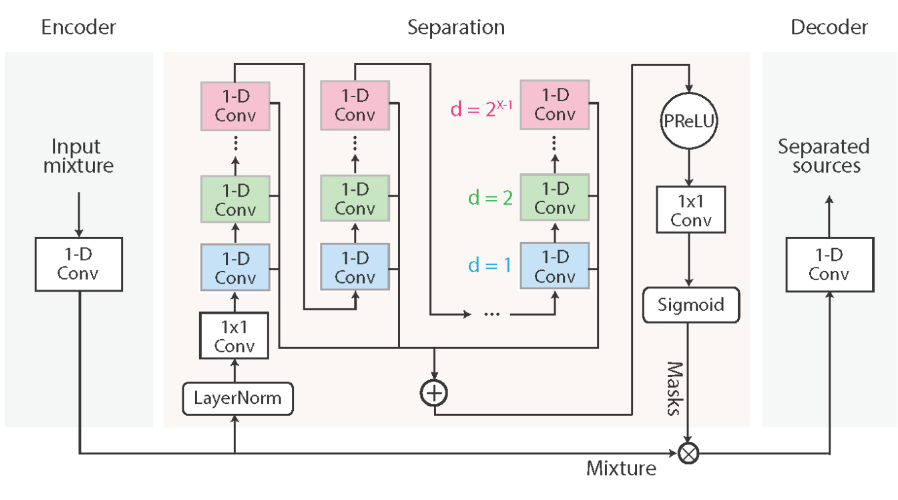
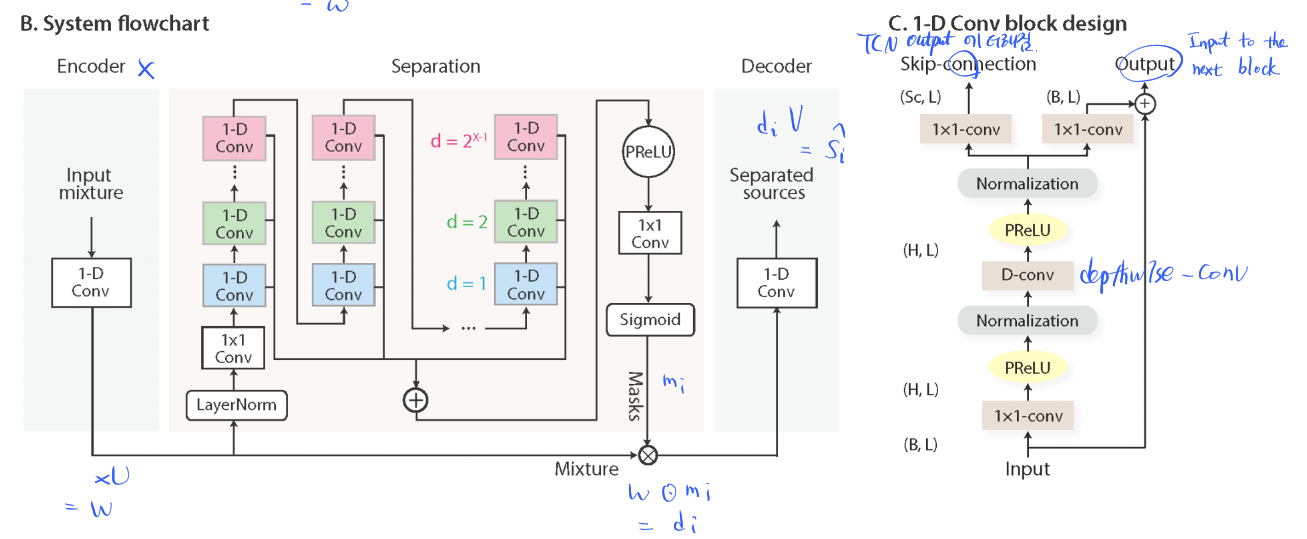
2. Convolutional Time-domain Audio Separation Network
- Estimating $C$ sources $s_1(t), ..., s_c(t) \in \mathbb{R}^{1 \times T}$ from $x(t) \in \mathbb{R}^{1 \times T}$, where
$$x(t)=\sum_{i=1}^Cs_i(t)$$
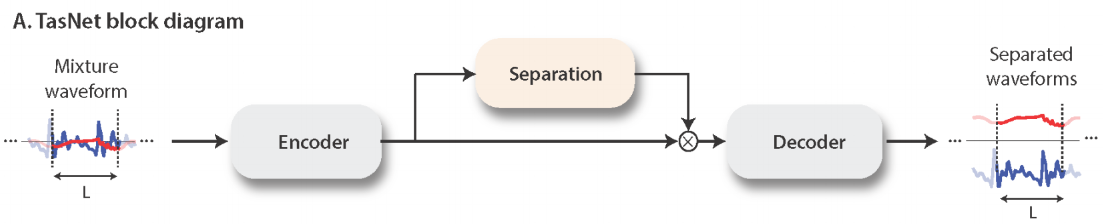
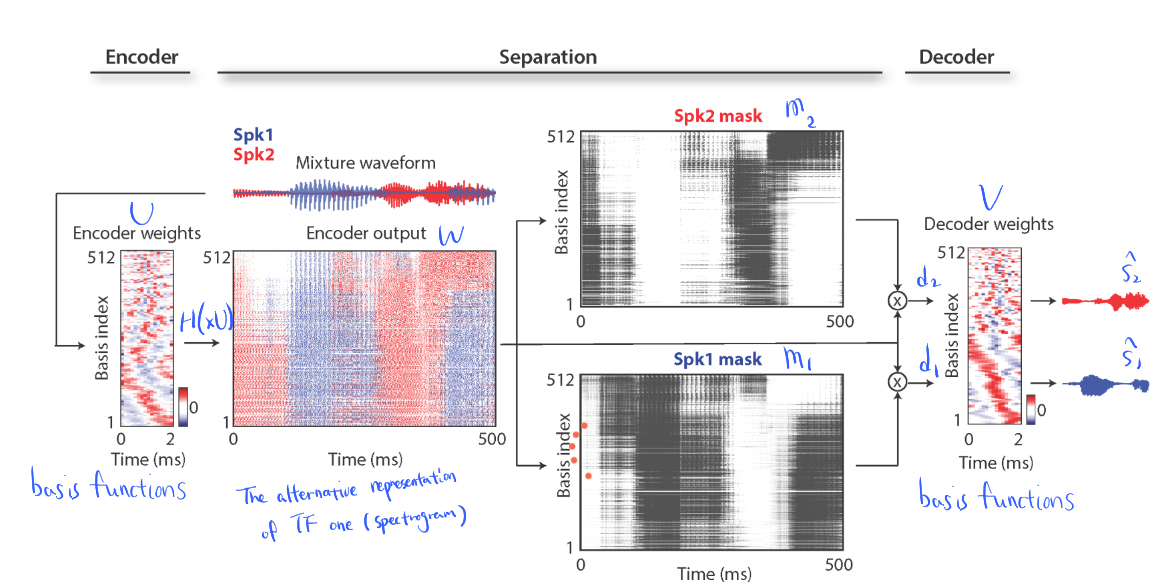
Encoder
$\mathbf{x}$ (==$\mathbf{x}_k$) is transformed into $\mathbf{w}$ by 1-D convolution
$\mathbf{w}=\mathcal{H}(\mathbf{xU})$
- $\mathbf{x}$ (==$\mathbf{x}_k$) is a segmented waveforms
- $\mathbf{U}$ contains $N=512$ vectors (encoder basis functions) with length $L$ each
- $\mathcal{H}()$ is (optional) nonlinear functions
- Pseudo-inverse, Linear, ReLU are used in the experiments
- Linear encoder (without $\mathcal{H}()$) are proven to perform best
class TasNet(nn.Module):
def __init__(self, enc_dim=512, feature_dim=128, sr=16000, win=2, layer=8, stack=3,
kernel=3, num_spk=2, causal=False):
super(TasNet, self).__init__()
...
# input encoder
self.encoder = nn.Conv1d(1, self.enc_dim, self.win, bias=False, stride=self.stride)
Separation module
- consists of stacked 1-D dilated convolution blocks
- Each layer in a TCN consists of 1-D conv blocks with increasing dilation factors
Decoder
reconstructs the waveform $\mathbf{\hat x}$, from $\mathbf{w}$, by 1-D transposed convolution
$\mathbf{\hat x} = \mathbf{wV}$
- $\mathbf{\hat x}$ is the reconstruction of $\mathbf{x}$
- $\mathbf{V}$ contains $N=512$ vectors (decoder basis functions) with length $L$ each
class TasNet(nn.Module):
def __init__(self, enc_dim=512, feature_dim=128, sr=16000, win=2, layer=8, stack=3,
kernel=3, num_spk=2, causal=False):
super(TasNet, self).__init__()
...
# output decoder
self.decoder = nn.ConvTranspose1d(self.enc_dim, 1, self.win, bias=False, stride=self.stride)
...How is Separation done?
- Estimation from $C$ vectors (== masks) $\mathbf{m}_i$
- $C$(==number of speakers)
- $\mathbf{m}_i$ is the output from the Separation module
- $\mathbf{m}_i$ is then multiplied by $\mathbf{w}$ in an element-wise manner
- $\mathbf{d}_i = \mathbf{w} \odot \mathbf{m}_i$
- $\mathbf{d}_i$ is the input to the Decoder
- $\mathbf{\hat s}_i = \mathbf{d}_i \mathbf{V}$$\mathbf{d}_i$ is then multiplied by $\mathbf{V}$ to become an estimated waveform $\mathbf{\hat s}_i$
3. Experiments
Datasets - Wall Street Journal (WSJ)
- WSJ0-2mix for two-speaker separation
- WSJ0-3mix for three-speaker separation
- generating mixtures
- resampled at 8kHz
- randomly choosing utterances from different speakers
- randomly choosing SNR between -5 and 5dB
Experiment configurations
- 100 epochs on 4-second segments
- initial lr=$1e^{-3}$
- Adam optimizer
- 50% stride size (== 50% overlap between frames)
Training objective
- maximizes scale-invariant source-to-noise ratio (SI-SNR)
- SI-SNR
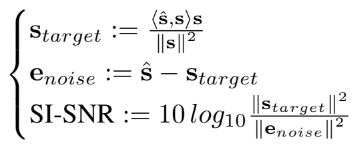
SDR – HALF-BAKED OR WELL DONE? (https://arxiv.org/pdf/1811.02508.pdf)
Comparison with ideal TF masks
- Ideal binary mask (IBM)
- Ideal ratio mask (IRM)
- Wiener filter-like mask (WFM)where $\mathcal{S}_i(f,t) \in \mathbb{C}^{F \times T}$ are complex spectrograms
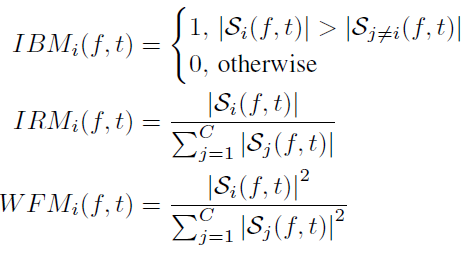
- configurations
- 32ms window size, Hanning window
- 8ms hop size
4. Results
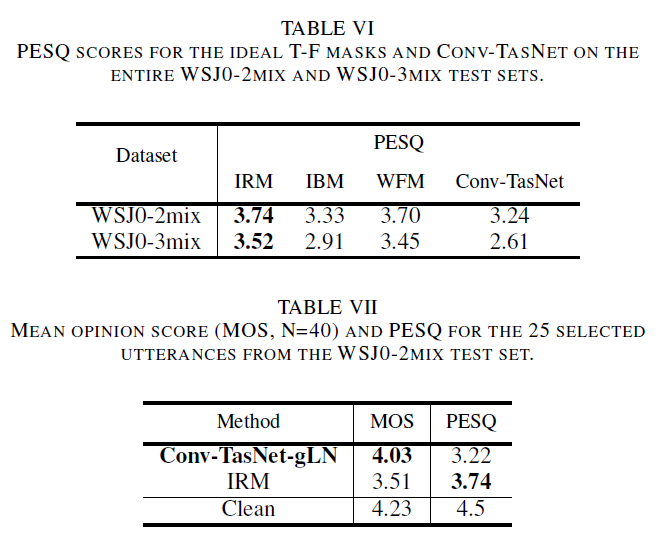
Comparison with previous methods
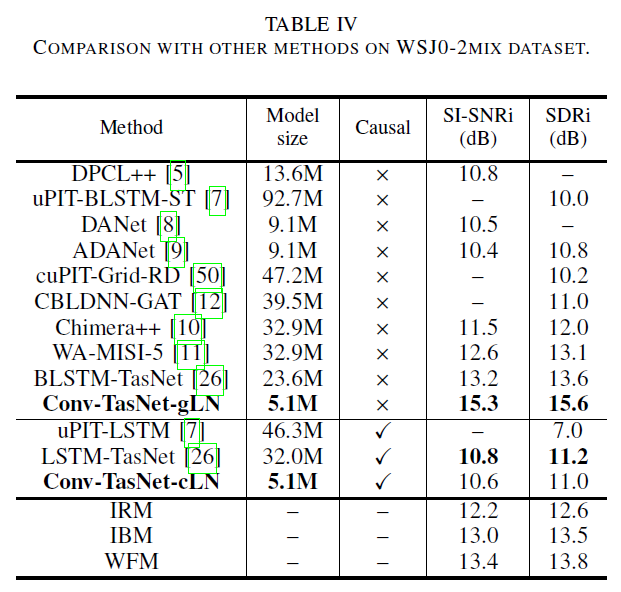
- noncausal Conv-TasNet surpasses all three ideal TF masks
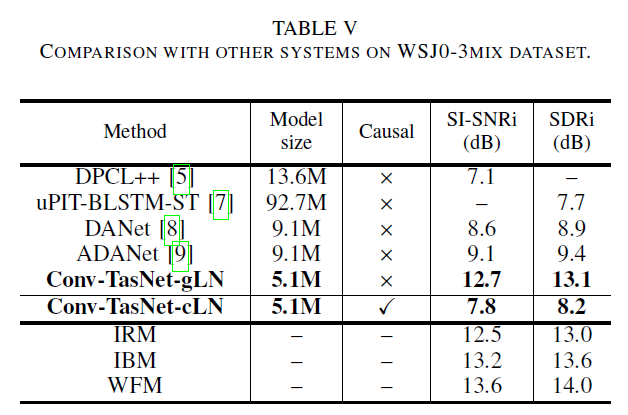
- noncausal Conv-TasNet outperforms all STFT-based systems
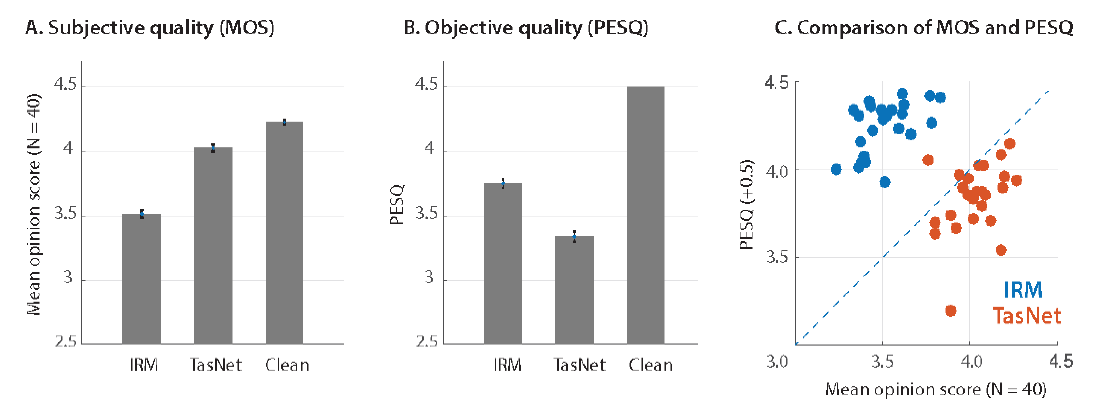
Subjective and objective quality evaluation
- PESQ: Perceptual Evaluation of Speech Quality
- aims to predict the subjective quality of speech
5. Questions and Comments
- Ideal TF masks vs STFT-based systems
- Ideal TF masks는 전통적인 신호처리 방식을 일컫는 것인가? 혹은 딥러닝 방법론도 포함하는 것인가?
- Ideal TF masks $\subset$ STFT-based system 인 것인가?
- PESQ의 정확한 metric이 무엇인가?
'컴퓨터비전 : CV > CNN based' 카테고리의 다른 글
| [논문 리뷰] Going Deeper with Convolutions (0) | 2022.08.13 |
|---|---|
| [논문 리뷰] SiamRPN++: Evolution of Siamese Visual Tracking with Very Deep Networks (0) | 2022.05.08 |
| [논문 리뷰] Mask R-CNN (0) | 2022.03.20 |
| [논문 리뷰] Retina Net : Focal loss (0) | 2022.03.12 |
| [논문 리뷰] FPN : Feature Pyramid Network (0) | 2022.03.12 |




