Notice
| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | ||
| 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 13 | 14 | 15 | 16 | 17 | 18 | 19 |
| 20 | 21 | 22 | 23 | 24 | 25 | 26 |
| 27 | 28 | 29 | 30 |
Tags
- Fast RCNN
- YAI 11기
- CS224N
- transformer
- RCNN
- NLP
- rl
- cl
- PytorchZeroToAll
- nerf
- YAI 9기
- CNN
- 강화학습
- 자연어처리
- YAI
- YAI 8기
- 연세대학교 인공지능학회
- VIT
- GAN #StyleCLIP #YAI 11기 #연세대학교 인공지능학회
- YAI 10기
- cv
- Perception 강의
- 컴퓨터비전
- Faster RCNN
- NLP #자연어 처리 #CS224N #연세대학교 인공지능학회
- GaN
- 컴퓨터 비전
- 3D
- Googlenet
- CS231n
Archives
- Today
- Total
연세대 인공지능학회 YAI
[논문 리뷰] Retina Net : Focal loss 본문
FPN + RetinaNet (Focal Loss) - (2)
** YAI 9기 조용기님이 비전 논문 심화팀에서 작성한 논문입니다.
RetinaNet (Focal Loss)
Papers with Code - RetinaNet Explained
1. Introduction

2020년 전까지의 object detecton milestones. 출처 : Murthy, C.B et al., Investigations of Object Detection in Images/Videos Using Various Deep Learning Techniques and Embedded Platforms—A Comprehensive Review. Applied Sciences. 2020.
- 당시의 SOTA object detector는 two-stage의 proposal 매커니즘에 기반했다.
- R-CNN과 같이, 첫 번째 stage는 객체 위치 후보의 sparse set을 생성하고 두 번째 stage는 CNN을 사용하여 각 후보 location을 foreground나 background로 분류한다.
- 다른 one-stage detector에서는 비슷한 성능을 얻지 못했다.
- One stage detector는 객체의 위치와 스케일, 종횡비에 대한 regular, dense sampling에 적용되는 모델이다.
- YOLO나 SSD와 같은 one-stage detector는 SOTA two-stage 방법에 비해 10% ~ 40%의 낮은 정확도에서 빠른 탐지 작업을 수행한다.
- 이 논문에서 제안한 one-stage detector는 이러한 one-stage 방식의 한계를 넘어, two-stage detector들과 필적하는 성능을 보여준다.
- 이를 위해 논문에서는 훈련 중의 class imbalance를 one-stage detector가 SOTA의 정확도를 가지지 못하게 하는 주된 장애물로 판단하고, 이를 제거하는 새로운 손실 함수를 제안한다.
- Two-stage 방식의 경우 다음과 같이 class imbalance를 해결했다:
- Proposal stage (Selective Search, EdgeBoxes, DeepMask, RPN) : Object location 후보의 수를 빠르게 줄이며 대부분의 background 샘플을 제외한다.
- Classification stage : Heuristic (e.g., fixed foreground-to-background ratio)이나 online hard example mining (OHEM)과 같은 작업을 수행하여 foreground와 background 사이의 균형을 조절한다.
- 대조적으로, one-stage detector는 이미지 전체에서 규칙적으로 샘플링된 object location 후보의 dense set를 처리해야 한다.
- Sampling heuristic이 적용될 수 있지만, 훈련 절차가 여전히 background 샘플로 지배되므로 비효율적이다.
- 이러한 비효율은 bootstraping이나 hard example mining과 같은 기술을 통해 해결될 수 있는 객체 탐지의 고전적인 문제였다.
- 이 논문에서는 class imbalance를 다루기 위해, 이전의 접근 방식보다 더 효과적으로 작용하는 손실 함수인 Focal Loss를 제안했다.
- 이 함수는 올바른 클래스에 대한 신뢰도가 증가함에 따라 scaling factor가 0으로 감소하는, 동적 스케일의 크로스 엔트로피 손실이다. 훈련 중에 easy example의 기여도를 자동으로 낮추고 모델이 hard example에 빠르게 집중하도록 한다.
- 이 Focal Loss는 one-stage detector가 앞선 기술들의 성능을 능가하는 높은 정확도를 가지도록 훈련시켰다.
- 또한 논문에서는 focal loss의 효율성을 입증하기 위해 간단한 one-stage object detector인 RetinaNet을 설계했다.
- 신경망 내의 효율적인 feature pyramid와 anchor box를 특징으로 한다.
2. Related Work
Classic Object Detectors
- Dense image grid에 classifier를 적용하는 sliding-window 패러다임은 길고 풍부한 역사를 가지고 있다.
- 초기 detector 중 하나는 LeCun et al.의 작업으로, 손글씨 숫자 인식에 CNN을 적용했다.
- Viola와 Jones는 얼굴 인식에 현재 광범위하게 사용되는 boosted object detector를 사용했다.
- HOG와 integral channel features의 도입은 보행자 탐지를 위한 효과적인 방법을 이끌어냈다.
- DPM은 dense detector가 더 일반적인 객체 범주로 확장하는데 도움을 주었고, 수 년 동안 최고의 결과를 보여주었다.
- Sliding-window 접근 방법이 고전 컴퓨터 비전의 주요 탐지 패러다임이었지만, two-stage 방식이 빠르게 객체 탐지를 지배하게 되었다.
Two-stage Detectors
- 현대 객체 탐지에서 지배적인 패러다임은 two-stage 접근 방법이다.
- 대표적인 Selective Search와 같이, 첫 번째 stage는 대부분의 negative location을 제외하면서 모든 객체를 포함하는 후보 proposal의 sparse set을 생성하고, 두 번째 stage는 proposal을 foreground/background 클래스로 분류한다.
- R-CNN은 CNN을 사용하여 두 번째 stage classifier의 정확도를 크게 향상시키며 현대 객체 감지 시대를 열었다.
- 이 R-CNN은 몇 년동안 속도 면에서 학습된 object proposal을 사용하여 개선되었다.
- Region Proposal Network (RPN)은 두 번쨰 stage classifier를 사용한 object proposal을 하나의 CNN에 통합하여 Faster R-CNN 프레임워크의 기반이 되었다.
One-stage Detectors
- OverFeat는 깊은 신경망에 기반한 현대적인 초기 one-stage object detector이다. 최근에는 SSD와 YOLO가 one-stage 방법에 대한 관심을 다시 불러일으켰다.
- 이 방식은 빠른 속도 를 가지고 있지만, two-stage 방식에 비해 정확도가 좋지 않다.
- Two-stage 방식은 지속적인 개선으로 입력 이미지의 해상도와 proposal 수를 줄여 속도를 빠르게 만들 수 있는 반면, one-stage 방법은 여전히 계산 양이 많고 정확도도 뒤떨어졌다.
- 이 방식은 빠른 속도 를 가지고 있지만, two-stage 방식에 비해 정확도가 좋지 않다.
- 따라서 이 논문의 목적은 one-stage detector가 two-stage detector에 비해서 비슷하거나 더 좋은 속도와 정확도를 얻는 것이다.
- RetinaNet의 디자인은 이전의 dense detector와 많은 유사성을 가진다.
- 특히 RPN에서 도입된 ‘anchor’와 SSD와 FPN에서의 feature pyramid 사용 방식이 그렇다.
- 이 논문에서는 신경망 설계에서의 혁신이 아니라, 새로 도입된 손실 함수로 detector가 최고의 결과를 보여주었다고 강조하고 있다.
Class Imbalance
- 고전적인 one-stage 객체 탐지 방법(boosted detector, DPM)과 최근의 방법들(SSD)은 커다란 class imbalance에 직면한다.
- One-stage detector들은 이미지당 104 ~ 105개의 후보 location을 탐지하지만, 객체가 포함된 location은 소수에 불과하다.
- 이러한 imbalance는 두 가지 문제를 야기한다:
- 대부분의 location이 학습에 유용한 기여가 아닌 easy negative 이므로 훈련이 비효율적이다.
- 이 많은 easy negative가 훈련을 압도하여 모델을 퇴화시킬 수 있다.
- 이에 대한 일반적인 해결책은 훈련 중에 hard example을 샘플링하는 hard negative mining 이나 다른 복잡한 sampling/reweighing scheme이다.
- 이와는 다르게, 이 논문에서 제안된 focal loss는 class imbalance를 자연스럽게 처리하고 샘플링과 easy negative 없이 모델이 모든 샘플에 효율적으로 훈련이 되도록 한다.
Robust Estimation
- Robust loss function (e.g., Huber Loss)은 커다란 error를 보이는 hard example의 가중치를 줄여 outlier의 기여를 줄이는 손실이다.
- 대조적으로 focal loss는 outlier를 다루기보다 inlier, 즉 easy example의 가중치를 줄여 그 수가 많더라도 그 기여를 작도록 함으로 class imbalance를 해결한다.
- Focal loss는 robust loss의 반대 역할을 수행하며, hard example의 sparse set에서의 훈련에 집중한다.
3. Focal Loss
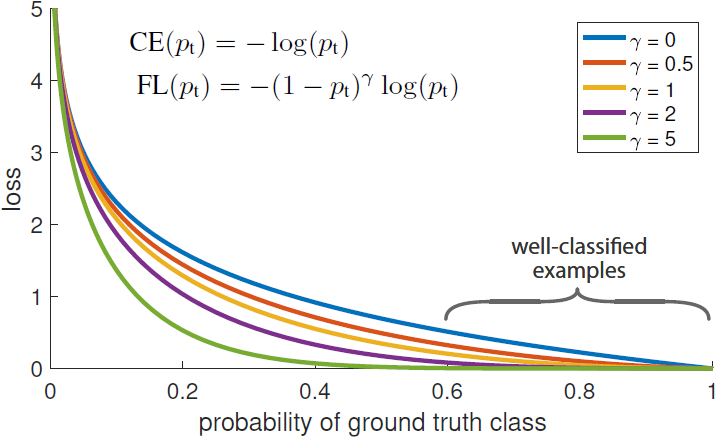
Figure 1. We propose a novel loss we term the Focal Loss that adds a factor (1−pt)γ to the standard cross entropy criterion. Setting γ>0 reduces the relative loss for well-classified examples (pt>.5), putting more focus on hard, misclassified examples. As our experiments will demonstrate, the proposed focal loss enables training highly accurate dense object detectors in the presence of vast numbers of easy background examples.
- Focal Loss는 훈련에서 foreground/background 클래스 사이 극도의 불균형이 존재하는 (e.g., 1:1000) one-stage 객체 탐지 시나리오를 다루도록 설계되었다. 논문에서는 이 손실을 간단히 이진 분류에 사용되는 크로스 엔트로피 (cross entropy, CE) 에서 부터 시작하며 소개한다 (다중 클래스에 대해서도 손쉽게 확장이 가능하다):
- y∈±1은 ground-truth 클래스이다.
- p∈[0,1]은 모델이 레이블이 y=1인 (양성) 클래스에 대해 추정한 확률이다.
- 간단한 표기를 위해 pt를 다음과 같이 정의한다:
- pt={pif y=1 1−potherwise,
- 따라서 CE(p,y)=CE(pt)=−log(pt)로 표현할 수 있다.
- CE(p,y)={−log(p)if y=1 −log(1−p)otherwise,
- CE 손실은 Figure 1의 파란 곡선에 해당한다.
- 그림에서 well-classified example에도 사소하지 않은 크기의 손실이 존재하는 것을 볼 수 있다.
- 따라서 많은 수의 easy example이 모이면 작은 크기의 손실로도 rare class를 압도할 수 있다.
3.1. Balanced Cross Entropy
- Class imbalance를 처리하는 일반적인 방법은 가중치 α∈[0.1]를 클래스 1에, 1−α를 클래스 −1에 추가하는 것이다.
- 실제로는 α가 inverse class frequency로 설정되거나 교차 검증에서 설정된 하이퍼파라미터로 처리된다.
- 간단한 표기를 위해 pt를 정의한 것처럼 αt를 정의한다.
- α-balanced CE 손실은 다음과 같다:
- CE(pt)=−αtlog(pt).
- 이 손실은 CE의 간단한 확장으로 focal loss의 실험 기반이다.
3.2. Focal Loss Definition
- Dense detector 훈련 중에 마주치는 class imbalance는 CE 손실을 압도한다.
- Easy negative는 손실의 대부분을 구성하고 그래이디언트를 지배한다.
- α가 positive/negative example의 중요성에 균형을 맞추지만, easy/hard example을 구별하지는 않는다.
- 따라서 논문에서는 easy example의 가중치를 낮추며 hard negative의 훈련에 집중하도록 손실 함수를 재구성한다.
- Focal loss는 다음과 같이 정의되며, Figure 1에서 몇 가지 γ∈[0,5]에 대해 시각화되었다:
- (1−pt)γ는 CE 손실에 대해 추가한 modulating factor이다.
- γ≥0은 조정이 가능한 focusing parameter이다.
- FL(pt)=−(1−pt)γlog(pt)
- Focal loss는 다음과 같은 특성이 있다:
- Example이 잘못 분류되고 pt가 작으면 modulating factor가 1에 근접하고 손실은 영향을 받지 않는다. pt가 1에 근접하면 modulating factor는 0에 근접하게 되고 따라서 잘 분류된 examp[le에 대한 가중치가 줄어든다.
- Focusing parameter γ는 easy example의 가중치를 줄이는 비율을 조정한다. γ=0일 때 FL 손실은 CE와 같으며, γ가 증가함에 따라 modulating factor의 영향도 증가한다 (실험 결과 γ=2일 때 가장 잘 작동했다).
- 직관적으로, modulating factor는 easy example의 손실에 대한 기여를 줄이며, 샘플이 낮은 손실을 갖는 범위를 확장한다.
- γ=2일 때, pt=0.9로 분류되는 샘플은 CE에 비해 100배 낮은 손실을 가지며 pt≈0.968일 때 1000배 더 낮은 손실을 가진다.
- 이는 결국 잘못 분류된 샘플 교정의 중요성을 키운다 (pt≤.5,γ=2일 때 손실은 최대 4배 축소된다.).
- 실제로는 focal loss의 α-balanced variant를 이용하며 α를 추가한 형태가 정확도를 더 향상시켰다:
- 손실 레이어의 구현에서 p 계산을 위한 시그모이드 연산을 손실 계산과 결합하여 더 큰 수치적 안정성을 가져온다.
- FL(pt)=−αt(1−pt)γlog(pt).
- 논문에서 진행된 실험에서는 focal loss에 위와 같은 정의를 사용했지만, 정확한 형태는 중요하지 않다.
- 부록에서 focal loss의 다른 초기화와 이들의 효과를 소개했다.
3.3. Class Imbalance and Model Initialization
- 이진 분류 모델은 기본적으로 y=−1 또는 y=1을 똑같은 확률로 출력하도록 초기화된다.
- 이 때 class imbalance가 존재하면 frequent 클래스로 인한 손실이 전체 손실을 점유하고 초기 훈련에서의 불안정성을 야기한다.
- 이에 대응하기 위해 모델이 훈련 시작시 rare 클래스에 대해 추정한 값 p에 대한 ‘prior’를 도입한다.
- Prior probability (https://blog.mond.page/48)
- Prior는 π로 표기하며 모델이 샘플에 대해 추정한 p 값이 낮아지도록 (e.g. 0.01) 설정한다.
- 이는 모델 초기화의 변경 사항이며 (section 4.1) 손실 함수의 변경이 아니다.
- 이러한 변화는 class imbalance에서 CE와 FL 손실 모두에서 훈련 안정성을 향상시켰다.
3.4. Class Imbalance and Two-stage Detectors
- Two-stage detector는 주로 CE 손실로 훈련되며, α-balancing이나 제안된 손실을 사용하지 않는다. 그 대신 class imbalance를 두 가지 매커니즘으로 해결한다:
- Two-stage cascade : 첫 번째 cascade stage는 거의 무한에 가까운 object location 후보군을 1~2000개로 줄이는 object proposal 매커니즘이다. 이 때 중요한 점은 proposal은 무작위로 선택되지 않으며 실제 object location와 일치할 가능성이 높으므로 대부분의 easy nagative는 제거된다는 것이다.
- Biased mini-batch sampling : 두 번째 stage를 훈련시킬 때 biased sampling을 사용하며 양성 대 음성 비율이 (1:3 정도로) 편향된 미니배치를 구성하는데 사용된다. 이 비율은 샘플링을 통해 구현되는 일종의 implicit α-balancing factor처럼 생각할 수 있다.
- Focal loss는 one-stage 탐지 시스템에서 이러한 매커니즘을 처리하도록 설계되었다.
4. RetinaNet Detector
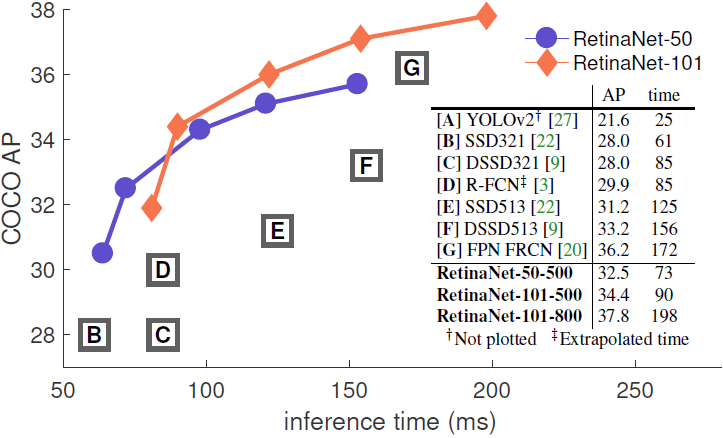
Figure 2. Speed (ms) versus accuracy (AP) on COCO test-dev. Enabled by the focal loss, our simple one-stage RetinaNet detector outperforms all previous one-stage and two-stage detectors, including the best reported Faster R-CNN [28] system from [20]. We show variants of RetinaNet with ResNet-50-FPN (blue circles) and ResNet-101-FPN (orange diamonds) at five scales (400-800 pixels). Ignoring the low-accuracy regime (AP<25), RetinaNet forms an upper envelope of all current detectors, and an improved variant (not shown) achieves 40.8 AP. Details are given in §5.
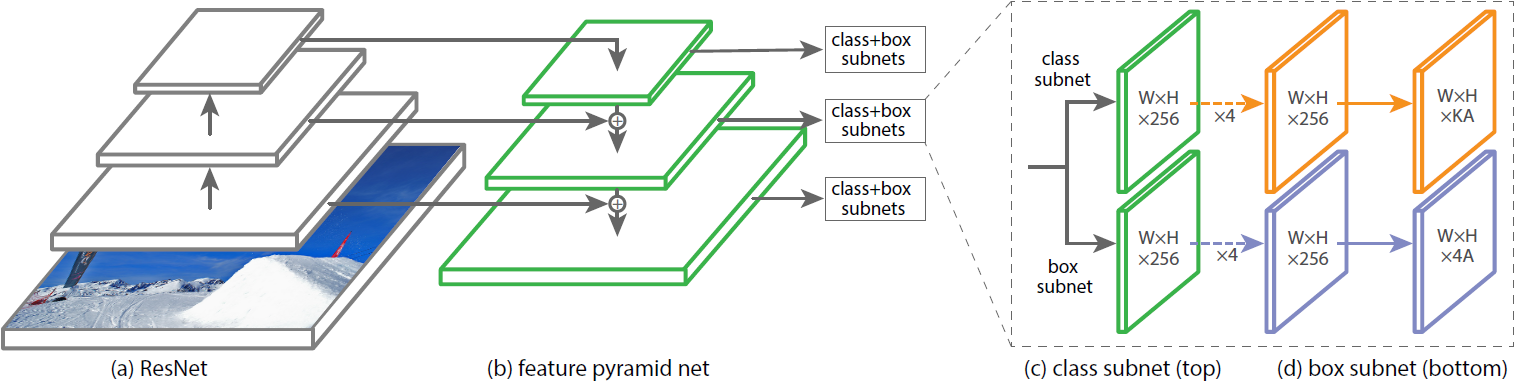
Figure 3. The one-stage RetinaNet network architecture uses a Feature Pyramid Network (FPN) [20] backbone on top of a feedforward ResNet architecture [16] (a) to generate a rich, multi-scale convolutional feature pyramid (b). To this backbone RetinaNet attaches two subnetworks, one for classifying anchor boxes (c) and one for regressing from anchor boxes to ground-truth object boxes (d). The network design is intentionally simple, which enables this work to focus on a novel focal loss function that eliminates the accuracy gap between our one-stage detector and state-of-the-art two-stage detectors like Faster R-CNN with FPN [20] while running at faster speeds.
- RetinaNet은 backbone network와 두 개의 subnetwork로 구성된 하나의 통합 신경망이다.
- Backbone network : 전체 입력 이미지에 대한 convolutional feature map을 계산하는 자체적인 convolution 신경망이다.
- Class subnetwork : backbone의 출력에 대해 convolutional object classification을 수행한다.
- Box subnetwork : convolutional bounding box regression을 수행한다.
- 두 subnetwork는 one-stage의 dense detection을 특징으로 한다.
Feature Pyramid Network Backbone
- 논문에서는 RetinaNet의 backbone으로 Feature Pyramid Network (FPN)을 채택했다.
- FPN은 표준 CNN을 top-down pathway와 lateral connection으로 확장하여 신경망이 단일 해상도의 입력 이미지에서 다중 스케일 feature pyramid를 효과적으로 구성하도록 한다 (Figure 3a, b).
- Pyramid의 각 level은 서로 다른 스케일의 객체를 탐지하는데 사용된다.
- FPN은 fully convolutional network (FCN)의 다중 스케일 예측을 개선했다.
- RetinaNet에서는 FPN 논문에서 사용한 ResNet 아키텍처를 사용했으며, P3부터 P7까지의 pyramid를 구성했다.
- ResNet의 마지막 레이어만 사용했을 때는 낮은 성능을 보였다. 따라서 FPN backbone을 사용한다.
Anchors
- 논문에서는 FPN의 RPN 변형에 있는 것과 유사한 transition-invariant anchor box를 사용한다.
- Anchor의 면적은 P3부터 P7까지 각각 322부터 5122이며, 종횡비는 1:2,1:1,2:1이다.
- Dense scale을 위해, 각 level의 3개의 종횡비에 대한 세트에 크기 20,21/3,22/3을 추가한다.
- 따라서 level별로 A=9개의 anchor가 있으며, level 전반에 걸쳐 입력 이미지에 따라 32 ~ 813 픽셀 스케일 범위를 다룬다.
- 각 anchor는 길이 K인 (K는 클래스 개수) one-hot classification target vector와 길이 4의 box regression target vector로 할당된다.
- 논문에서는 기본적으로 RPN의 할당 규칙을 사용하지만 다중 클래스 탐지를 위해 몇 가지 사항이 수정되었다.
- Anchor는 intersection-over-union (IoU) threshold 0.5를 사용하여 ground-truth에 할당되며 [0,0.4)에 속한 경우 background로 할당된다. Overlap이 [0.4,0.5) 사이인 경우, 훈련 중에 무시된다.
- Box regression target은 anchor와 할당된 객체의 box 사이의 offset으로 계산되거나, 할당된 객체가 없는 경우 생략된다.
Classification Subnet
- Classification subnet은 각 A개의 anchor와 K개의 object class에 대해 각 위치에서 객체가 존재할 확률을 예측한다.
- 이 subnet은 각 FPN level에 연결된 작은 FCN이며, subnet의 파라미터는 모든 pyramid level 사이에 공유된다.
- 주어진 pyramid level로부터 C 채널의 입력 feature map을 받아 C filter의 3×3 conv layer, ReLU, 그 후 KA filter의 3×3 conv layer를 통과한다. 마지막으로 위치별 KA개의 이진 예측에 시그모이드 활성화 함수가 결합된다.
- 대부분의 실험에서 C=256,A=9을 사용했다.
- RPN과 다르게, 논문의 object classification subnet은 더 깊고, 3×3 conv layer만을 사용하며, box regression subnet과 파라미터를 공유하지 않는다.
- 실험 결과 이러한 디자인적인 선택이 특정한 하이퍼파라미터 값 선택보다 더 중요했다.
Box Regression Subnet
- Object classification subnet과 병렬적으로, 각 pyramid level에 다른 작은 FCN을 연결하여 근처에 각 anchor box로부터 근처 ground-truth 객체에 대한 offset을 예측한다.
- Subnet의 설계는 각 location에 대한 4A 선형 출력으로 끝난다는 점을 제외하면 classification subnet의 설계와 동일하다.
- 각 location의 A개의 anchor에 대해, 4개의 출력은 anchor와 ground-truth box 사이 offset을 예측한다 (R-CNN의 표준 box 파라미터화를 사용했다).
- 최근 대부분의 작업과는 다르게, 논문에서는 class-agnostic bounding box regressor를 사용했으며 이는 더 적은 파라미터를 사용하면서도 똑같이 효과적이었다.
4.1. Inference and Training
Inference
- RetinaNet은 ResNet-FPN backbone과 classification/box regression subnet으로 구성된 단일 FCN이다.
- 추론에는 간단히 신경망에 이미지를 전달하면 된다.
- 논문에서는 속도 향상을 위해 detector의 신뢰도에 대해 threshold를 0.05로 설정한 후 FPN level마다 최대 1000개의 상위 예측으로부터 box 예측만 디코딩한다.
- 모든 level의 상위 예측이 병합되고 threshold 0.5의 비최대 억제가 적용되어 최종 탐지가 이루어진다.
Focal Loss
- 이 논문에서 도입된 focal loss는 classification subnet 출력의 손실로 사용되었다.
- Section 5에서 설명하듯이, 실제로 γ=2에서 모델이 잘 동작했으며 RetinaNet은 γ∈[0.5,5]에 상대적으로 robust했다.
- RetinaNet 훈련시 focal loss는 각 샘플링된 이미지에 대해 전체 ~100k anchor에 적용되었다.
- 이는 heuristic sampling (RPN)이나 hard example mining (OHEM, SSD)과 같이 각 미니배치에 대해 작은 anchor 세트를 선택하는 일반적인 방법과는 다르다.
- 이미지의 총 focal loss는 전체 ~100k anchor loss의 합으로 계산되며 이 합은 전체 anchor 수가 아닌 ground-truth box에 할당된 anchor 수로 정규화된다 (대다수의 anchor가 easy negative이며 focal loss에서 무시할 만한 손실 값을 갖는다).
- Rare 클래스에 할당되는 α 또한 안정적인 범위가 있지만 α가 γ와 상호작용하므로 두 파라미터를 함께 고려해야 한다.
- 일반적으로 α는 γ가 증가함에 따라 조금씩 감소해야 한다 (실험 결과 γ=2,α=0.25에서 최고 성능을 보였다).
Initialization
- RetinaNet subnet의 (마지막 레이어를 제외한) 모든 새로운 conv layer는 편향이 b=0, 가중치가 σ=0.01의 가우시안으로 초기화되었다.
- Classification subnet의 마지막 conv layer는 편향을 b=−log((1−π)/π)로 초기화했으며, 이 때 π는 훈련 시작시 모든 anchor가 ~π의 신뢰도로 foreground로 레이블되어야 함을 지정한다.
- 실험 결과가 π 값에 robust하므로 모든 실험에서 π=.01로 설정되었다.
- Section 3.3에서 설명했듯이, 이러한 초기화를 통해 많은 수의 background anchor가 커다란 불안정한 손실 값을 만드는 것을 방지한다.
Optimization
- RetinaNet은 stochastic gradient descent (SGD)로 훈련되었으며 0.0001의 가중치 감쇠와 0.9의 모멘텀이 적용되었다.
- 훈련 손실은 classification에 쓰인 focal loss와 box regression에 쓰인 표준 smooth L1 loss의 합이다.
5. Experiments
- 논문에서는 COCO 벤치마크의 bonding box detection track의 실험 결과를 보여주었다.
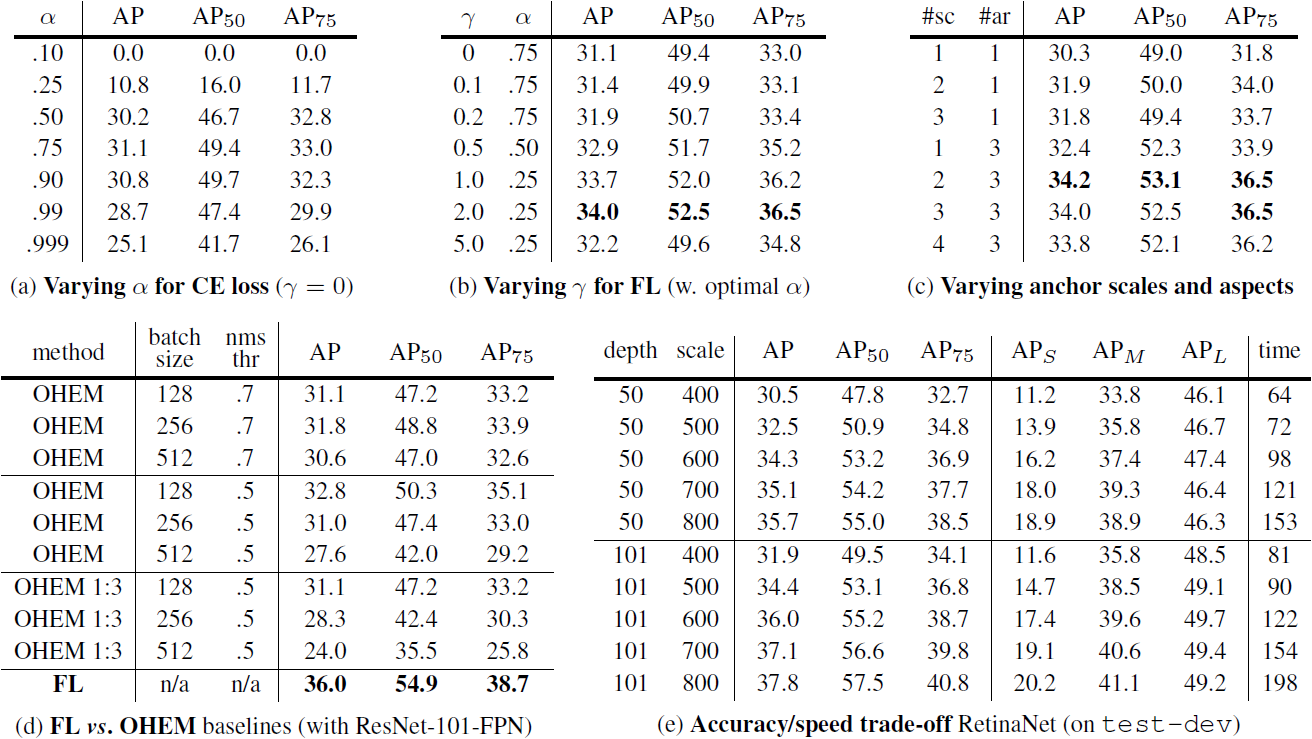
Table 1. Ablation experiments for RetinaNet and Focal Loss FL). All models are trained on trainval35k and tested on minival unless noted. If not specified, default values are: γ=2; anchors for 3 scales and 3 aspect ratios; ResNet-50-FPN backbone; and a 600 pixel train and test image scale. (a) RetinaNet with α-balanced CE achieves at most 31.1 AP. (b) In contrast, using FL with the same exact network gives a 2.9 AP gain and is fairly robust to exact γ/α settings. (c) Using 2-3 scale and 3 aspect ratio anchors yields good results after which point performance saturates. (d) FL outperforms the best variants of online hard example mining (OHEM) [31, 22] by over 3 points AP. (e) Accuracy/Speed trade-off of RetinaNet on test-dev for various network depths and image scales (see also Figure 2).
5.1. Training Dense Detection
- 실험을 통해 다양한 최적화 전략과 함께 dense detection에서 손실 함수가 어떻게 동작하는지를 분석했다.
- 모든 실험에 FPN이 추가된 ResNet-50/101을 사용했으며, 모든 ablation 실험에서는 훈련과 테스트 동안 600 픽셀의 이미지 스케일을 사용했다.
Network Initialization
- 첫 번째 시도에서는 어떠한 초기화와 학습 전략의 수정 없이 표준 CE 손실만 사용해 RetinaNet을 훈련시켰다.
- 이는 신경망이 훈련 도중 발산하여 실패했다.
- 간단히 마지막 레이어를 객체 탐지의 사전확률 (prior probability) π=.01이 되도록 초기화함으로 효과적인 학습이 가능하다.
Balanced Cross Entropy
- α=.75일 때 AP가 0.9 상승하는 모습을 보여주었다 (Table 1a).
Focal Loss
- Focal loss (FL)는 modulating term의 정도를 조절하는 focusing parameter γ를 도입한다 (Table 1b).
- γ=0일 때, 손실 함수는 CE 손실이 된다.
- γ가 증가하면 손실 그래프의 모양이 “easy” example의 손실 값이 줄어들도록 바뀐다 (Figure 1).
- FL은 γ가 증가하면서 CE보다 많은 성능 향상을 가져왔으며, γ=2일 때 FL이 α-balanced CE 손실에 비해서 2.9 AP 향상을 보였다.
- 실험을 통해서 각각의 γ에 대해 최고의 α를 찾아내었으며 γ가 커질 수록 선택된 α는 줄어들었다.
- Easy negative의 가중치가 줄어들기 떄문에 positive에 가해지는 가중치 또한 줄여야 한다고 볼 수 있다.
- γ를 고치는 것이 α를 고치는 것보다 큰 영향을 미치며 α의 유의미한 범위는 [.25,.75]였다 (논문에서는 α∈[.01,.999]를 측정했다).
- 모든 실험에서 γ=2.0,α=.25를 사용했다.
Analysis of the Focal Loss
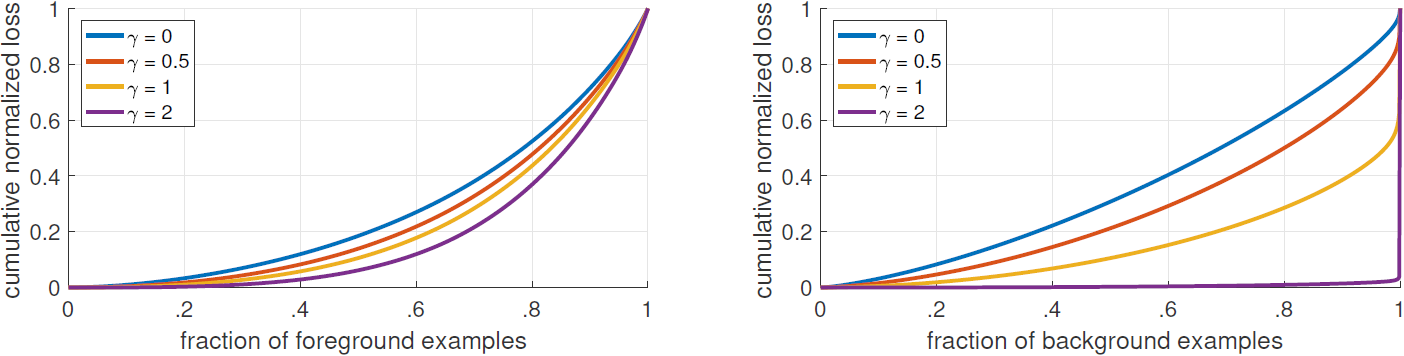
Figure 4. Cumulative distribution functions of the normalized loss for positive and negative samples for different values of γ for a converged model. The effect of changing γ on the distribution of the loss for positive examples is minor. For negatives, however, increasing γ heavily concentrates the loss on hard examples, focusing nearly all attention away from easy negatives.
- Focal loss의 더 나은 이해를 위해, 논문에서는 수렴한 (converged) 모델에서 손실의 경험적 분포 (empirical distribution)를 분석했다.
- γ=2로 훈련된 ResNet-101 600-pixel 모델을 사용했으며, ∼107의 negative window와 ∼105의 positive window의 예측 확률을 갖도록 무작위 이미지를 샘플링했다.
- 각 positive/negative에 따로 FL를 계산하고 합이 1이 되도록 정규화를 진행한 후 오름차순으로 정렬했다.
- 여러 가지 γ에서 positive/negative에 대해 정렬된 손실의 누적 분포 함수 (cumulative distribution function, CDF)를 그렸다 (Figure 4).
- Positive (foreground) example의 경우, 여러 가지 γ에 대해 CDF는 꽤 비슷한 분포를 이루고 있다.
- 예를 들어 거의 20%의 hardest positive sample이 전체 손실의 절반을 차지하는데, γ가 커질 수록 상위 20%의 샘플에 집중하지만 그 효과는 크지 않다.
- Negative (background) example의 경우에는 그래프 분포가 극적으로 다르다.
- γ=0의 경우 positive/negative CDF가 꽤 비슷하다.
- γ가 증가하면서 hard negative example에 상당한 가중치가 집중된다.
- γ=2일 때 대부분의 손실은 아주 일부분의 hard negative에서 나오고 있다.
- 이를 통해 FL은 easy negative가 주는 영향을 효과적으로 줄이며, 모델이 hard negative에 온전히 집중할 수 있도록 함을 알 수 있다.
Online Hard Example Mining (OHEM)
- “Training Region-based Object Detectors with Online Hard Example Mining”에서는 큰 손실을 가지는 샘플을 사용한 미니배치를 만들어 two-stage detector의 성능을 높히는 방법인 OHEM을 제안했다.
- 각 example에 손실 점수를 계산한다.
- 비최대 억제 (non-maximum suppression, nms)를 수행한다. Threshold와 배치 크기는 수정할 수 있다.
- 손실이 큰 순서대로 example의 미니배치를 구성한다.
- OHEM은 FL처럼 잘못 분류된 example에 더 강조를 두지만, easy example을 완전히 배제한다는 점에서 FL과는 다르다.
- 논문에서는 SSD의 OHEM 변형도 같이 구현했다.
- 모든 example에 nms를 적용하고 미니배치를 positive/negative 비율이 1:3이 되도록 구성했다.
- 두 OHEM 전략을 큰 class imbalance를 가지고 있는 one-stage detection에서 테스트했다 (Table 1d).
- 실험 결과, OHEM 전략 중 가장 좋은 성능을 낸 설정 (32.8 AP)보다 FL 손실을 적용한 모델이 (36.0 AP) 더 효과적이었다.
Hinge Loss
- 초기 실험에서는 pt에 hinge loss를 이용하여 훈련을 진행했다. 이 손실은 불안정하며 의미 있는 결과를 얻지 못했다.
5.2. Model Architecture Design
Anchor Density
- One-stage 탐지 시스템에서 가장 중요한 설계 요소는 detector가 가능한 이미지 box 공간을 얼마나 조밀하게 커버할 수 있는지다.
- Two-stage detector는 region pooling operation을 통해 임의의 위치, 스케일, 종횡비의 box를 분류할 수 있다.
- 이와는 대조적으로 one-stage detector는 고정된 sampling grid를 사용하기에, 다중의 ‘anchor’를 사용하여 다양한 스케일/종횡비의 box를 커버하는 것이 일반적인 접근이다.
- 논문에서는 각 spatial position과 FPN의 각 pyramid level에 사용되는 anchor의 스케일과 종횡비를 살펴보았다 (Table 1c).
- 각 위치별로 단일 정사각형 anchor에서부터, [20,21/4,22/4,23/4]의 4가지 스케일과 [0.5,1,2]의 3가지 종횡비를 가진 12가지 anchor까지 비교했다.
- 단일 정사각형 anchor로도 좋은 AP 점수 (30.3)를 얻었다.
- 3가지 스케일과 3가지 종횡비를 사용했을 때 AP 점수가 34.0으로 향상되었으므로 다른 실험에서는 이 설정을 사용했다.
- 실험에서 anchor의 수를 6~9개 이상으로 늘려도 성능의 추가적인 향상을 얻지 못했다.
- 이를 통해 two-stage 시스템이 이미지의 임의의 box를 분류할 수는 있지만, density에서 성능의 포화가 two-stage의 성능에 이점을 가져오지 않는다는 것을 알 수 있다.
Speed versus Accuracy
- Backbone 신경망이 클 수록 더 높은 정확도를 가져오지만, 추론 속도는 더 느려진다. 이는 입력 이미지의 스케일에서도 마찬가지이다.
- 논문에서는 이 두 가지 요소의 영향을 분석했다 (Table 1e). Figure 2에서 RetinaNet의 속도/정확도 트레이드오프 곡선, 그리고 최근의 논문과의 비교를 확인할 수 있다.
- FL을 사용한 RetinaNet이 다른 모든 방법보다 더 높은 성능을 보여주고 있음을 알 수 있다.
- 더 큰 스케일을 사용하더라도 모든 two-stage 접근 방법보다 높은 정확도를 보여주며 여전히 빠르다.
5.3. Comparison to State of the Art
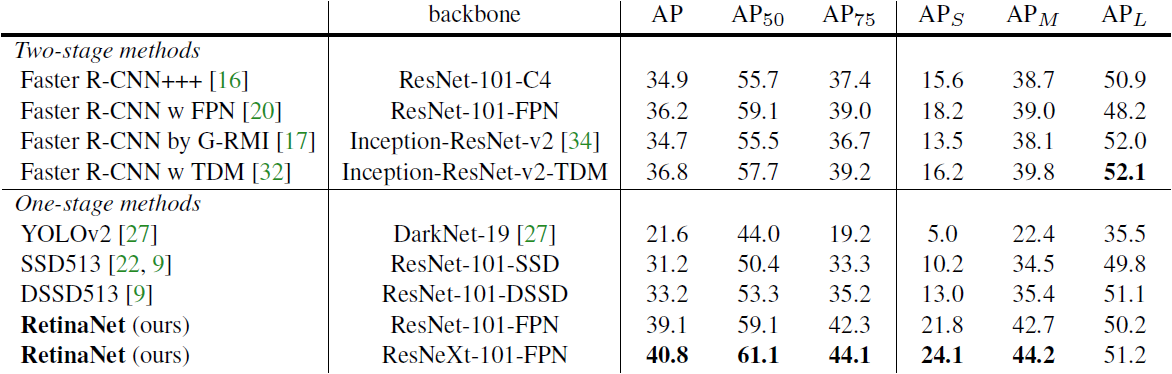
Table 2. Object detection single-model results (bounding box AP), vs. state-of-the-art on COCO test-dev. We show results for our RetinaNet-101-800 model, trained with scale jitter and for 1.5× longer than the same model from Table 1e. Our model achieves top results, outperforming both one-stage and two-stage models. For a detailed breakdown of speed versus accuracy see Table 1e and Figure 2.
Appendix A: Focal Loss*
- Focal loss의 정확한 형태는 중요하지 않다.
- 부록 A에서는 비슷한 특성과 결과를 가진, 본문의 FL과 다른 초기화 방법을 소개하며 보여준다.
- CE와 FL을 본문과 조금 다른 형태로 고려한다. 특히 quantity xt를 다음과 같이 정의한다:
- y∈±1은 본문과 같이 ground-truth 클래스이다.
- xt=yx.
- 따라서 pt=σ(xt)로 표기할 수 있으며 (이는 Equation 2에 부합한다), xt>0일 때 pt>.5로 올바르게 분류된다.
- p∗t와 FL의 alternate form FL∗을 다음과 같이 정의한다:FL∗=−log(p∗t)/γ.
- FL∗는 두 개의 파라미터 γ와 β를 가지며, 각각 손실함수의 steepness와 shift를 조절한다.
- p∗t=σ(γxt+β)
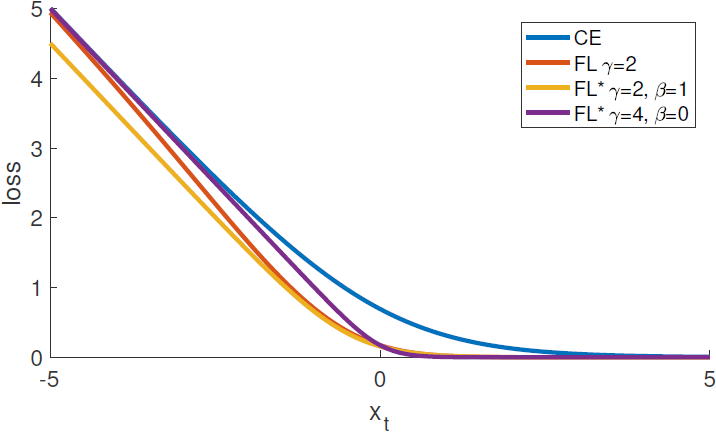
Figure 5. Focal loss variants compared to the cross entropy as a function of xt=yx. Both the original FL and alternate variant FL* reduce the relative loss for well-classified examples (xt>0).
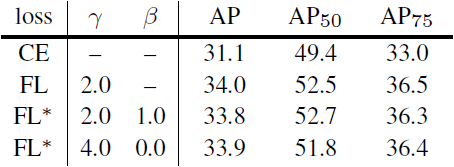
Table 3. Results of FL and FL* versus CE for select settings.
- Figure 5에서 CE와 FL, 그리고 FL*의 그래프 개형을 비교할 수 있다.
- FL*도 마찬가지로 잘 분류된 example에 할당되는 손실을 성공적으로 줄인다.
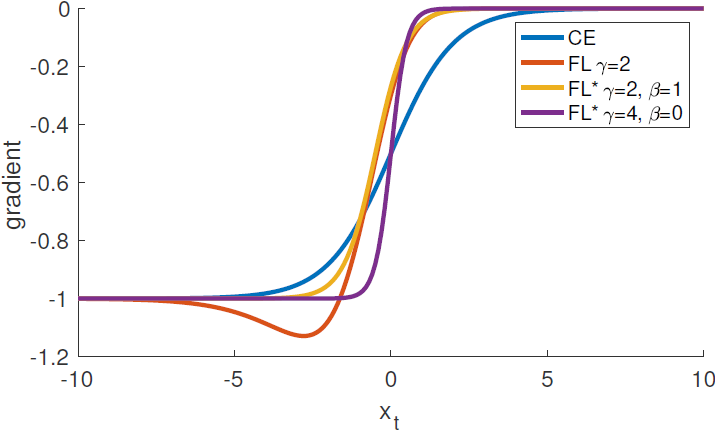
Figure 7. Effectiveness of FL* with various settings γ and β. The plots are color coded such that effective settings are shown in blue.
- 실험 결과 다양한 γ와 β 설정에서 좋은 결과를 얻을 수 있었다. - Figure 7에서 보았을 때, 잘 분류된 example (xt>0)에 대해 가중치를 적게 부여하는 손실 함수가 효과적임을 알 수 있다. - 일반적으로 FL이나 FL*과 비슷한 특성을 가진 임의의 손실 함수는 같은 효과를 보여줄 수 있다.
Appendix B: Derivatives
- CE, FL, 그리고 FL*의 x에 대한 미분은 다음과 같다:
- dCEdx=y(pt−1)
- dFLdx=y(1−pt)γ(γptlog(pt)+pt−1)
- dFL∗dx=y(p∗t−1)
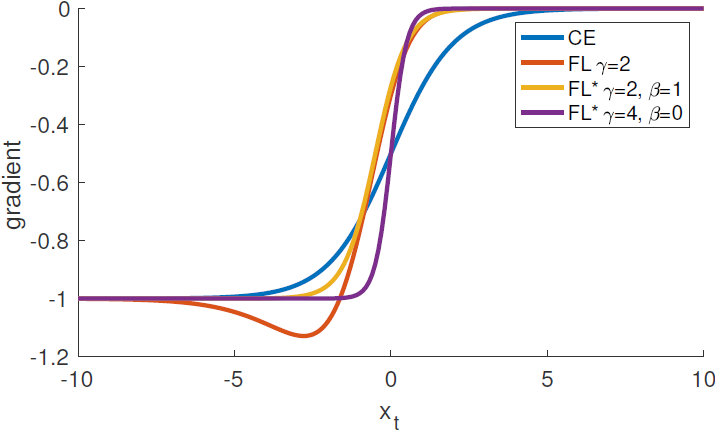
Figure 6. Derivates of the loss functions from Figure 5 w.r.t. x.
- 모든 손실 함수에서 도함수는 high-confidence prediction에서 -1 또는 0의 경향성을 보인다.
- 하지만 CE와는 다르게, FL과 FL*에서는 xt가 0 이상으로 증가하자마자 도함수의 크기가 바로 작아진다.
'컴퓨터비전 : CV > CNN based' 카테고리의 다른 글
| [논문 리뷰] SiamRPN++: Evolution of Siamese Visual Tracking with Very Deep Networks (0) | 2022.05.08 |
|---|---|
| [논문 리뷰] Mask R-CNN (0) | 2022.03.20 |
| [논문 리뷰] FPN : Feature Pyramid Network (0) | 2022.03.12 |
| [논문 리뷰] R-CNN / Fast R-CNN / Faster R-CNN (3) (0) | 2022.03.12 |
| [논문 리뷰] R-CNN / Fast R-CNN / Faster R-CNN (2) (0) | 2022.03.10 |




