| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | ||
| 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 13 | 14 | 15 | 16 | 17 | 18 | 19 |
| 20 | 21 | 22 | 23 | 24 | 25 | 26 |
| 27 | 28 | 29 | 30 |
- 강화학습
- VIT
- YAI 10기
- transformer
- NLP
- rl
- PytorchZeroToAll
- CS231n
- YAI
- Fast RCNN
- RCNN
- NLP #자연어 처리 #CS224N #연세대학교 인공지능학회
- CS224N
- 3D
- Perception 강의
- GaN
- 자연어처리
- YAI 11기
- YAI 8기
- CNN
- 컴퓨터비전
- nerf
- cv
- Faster RCNN
- Googlenet
- GAN #StyleCLIP #YAI 11기 #연세대학교 인공지능학회
- 연세대학교 인공지능학회
- cl
- 컴퓨터 비전
- YAI 9기
- Today
- Total
연세대 인공지능학회 YAI
[CS231N] DNN 기초 본문
DNN 기초
** YAI 10기 황채연님이 기초 심화 2팀에서 작성한 글입니다.
Introduction
지난 세선에서는 선형 분류기로 이미지를 분류하는 개념까지 다뤄보았다. 이미지가 가장 잘 분류되도록 기울기를 계속 갱신한다는 개념이었다. 그렇다면, 구체적으로 기울기 갱신은 어떻게 이루어지는가?
Loss fuction
Loss function은 손실을 정량적으로 알려주는 함수로, 어떤 기울기가 최선인지 결정하기 위해 loss를 컴퓨터가 자동 정량화하도록 고안된 함수이다.

인간은 좌측 그림과 loss 수치를 보고서 자동차, 고양이, 개구리 순으로 정확하게 분류되었다는 것을 파악할 수 있다. 이 판단 작업을 컴퓨터가 수행하기 위해 우측과 같은 식을 입력한다. 자세히 뜯어보면, N개의 x(이미지 픽셀 값)과 y(라벨) 세트의 loss를 계산할 때, 각 짝의 loss를 계산하고, 싹 다 더한 뒤, 세트의 개수로 나눠 평균을 구하면 된다. 이때 각 세트의 loss는 이미지 픽셀 값으로부터 도출된 예측값 f(x,W)(0
9)와 y(0
9)의 차이에서 계산된다.


Multiclass SVM loss
(S: 예측 점수 Yi: i번째 실제 클래스 Syi: i번째 실제 클래스의 점수)
어떤 클래스의 예측 점수에서 실제 클래스의 예측 점수를 빼서 1을 더한 값과 0 중 큰 값을 해당 클래스의 loss로 택한다. 0과 어떤값 중에 최댓값을 택하는 이런 손실 함수는 hinge loss라고 불리는데, loss가 점점 줄다가, loss가 충분히 작아지면 0으로 퉁친다고 보면 되겠다.

파란 점들을 지나는 그래프는 여러가지이다. 그중 그림과 같이 한 곡선에 대해 생각해보았을 때, 초록색의 새로운 데이터가 들어오면 예측이 아예 틀리게 된다. 그러므로 ‘occam’s razor’에 따라, 주어진 점을 지난다는 조건을 만족시키는 여러 그래프 중 가장 단순한 ‘직선’을 분류기로 채택하는 것이 옳다. 정규화 항을 손실 함수에 더해 가장 단순한 W가 채택되도록 한다. 이때 람다는 정규화 강도로, 튜닝의 대상인 하이퍼파라미터이다. 정규화의 방법은 아래와 같이 여러 종류가 있다.


Softmax


소프트맥스 손실 함수는 우선 score를 지수화해서, 모든 지수화시킨 score의 합에 대한 특정 지수화된 score의 비율에 마이너스 로그를 씌워서 손실을 계산한다. 왜 마이너스를 붙이느냐, 측정의 대상이 손실이기 때문에, 즉 손실이 클수록 이 손실 함수 값이 커지기를 원하기 때문에 마이너스 로그를 붙인다. 멀티클래스 SVM 손실 함수가 예측이 맞았는지 혹은 틀렸는지만 이분법적으로 도출해냈다면, 소프트맥스는 예측이 얼마만큼 틀렸는지 정량화해서 알려준다.
optimization

최적화는 마치 산 꼭대기에서 가장 낮은 곳으로 이동하는 것 같이, W를 갱신하는 것이다. 방법을 논해보면, 우선 랜덤으로 아무 W나 계속 넣어보고 결과를 관찰하는 방법이 있을 것이다. 아무런 규칙도 없는 이 방법이 좋은 효과를 가질리는 없다. 다른 방법으로는 경사를 따라가는 수가 있는데, 수학적으로는 각 x에 대한 유한 차분 근사, 즉 평균변화율의 극한값을 얻는 것이다. 그러나 이 수치적 경사 방법은 매우 비효율적이다. 경사를 따라가는 또다른 방법은 미분으로 dW식을 구해놓고 x를 대입만 하면 되는 분석적 경사 방법이 있다. 이 방법이 훨씬 빠를 것이다. 하지만 정확도는 수치적 경사 방법이 더 놓기 때문에, 우선 분석적 경사를 사용한 뒤 수치적 경사로 구현을 체크하는 방법을 사용한다.


Gradient descent


경사를 계산했으니, 이제 경사가 가장 클 때의 반대 방향으로 가면 가장 많이 내려갈 수 있다. 이때 중요한 것은 계산한 방향으로 얼마나 많이 이동할건진데, 한 걸음 당 보폭의 너비라고 생각하면 되겠다. 이 걸음 크기를 learning rate라고 한다. 그런데 학습 세트의 개수만큼 경사 하강해야 하므로 학습 세트가 많아지면 속도가 매우 느려질 수 밖에 없다. 이 문제의 해결책으로 확률적 경사 하강 (stochastic gradient descent) 가 사용된다. 즉, 전체 데이터에 대해 경사 하강을 진행하는 대신, 데이터의 일부에만 경사 하강을 진행하는 것이다. 이는 보통 2의 제곱수 32, 64 등의 크기를 가지는 미니 배치(mini batch)라고 불리는 학습 예제를 샘플링한다.
이미지 학습 방식


이미지 학습 방식에도 변화가 있었다. 기존에는 가공하지 않은 raw 이미지 픽셀(개구리 이미지)을 그대로 선형 분류기에 받아왔지만, 잘 작동되지 않았고, 따라서 raw 이미지의 feature represnetaion(개구리 이미지의 정량화된 값들)을 선형 분류기에 넣는 Image feature 방식이 개발되었다.
두 번째 사진의 좌측 그래프는 선형 분류기로 분류할 수 없기 때문에, 직교 좌표계 위에 표현된 점들을 극 좌표계로 옮긴다. 그럼 선형 분류가 가능해진다. Raw 이미지 픽셀을 극 좌표계로 옮길 순 없으니, 이미지에서 feature를 따와 극 좌표계로 옮기기로 한거다.


그렇다면 이미지에는 어떤 종류의 feature가 있을까? 첫 번째로, 색상 히스토그램이 있다. 각 색깔이 픽셀에서 얼마나 많이 나왔는지 알려준다. 두 번째로, 경사 히스토그램이 있다. 풀잎의 결 같은 이미지의 경사를 측정하는 것이다. 이를 측정하기 위해 이미지를 8X8 픽셀로 나눈 후, 픽셀 영역에서 가장 지배적인 엣지 방향을 양자화해서 여러 버킷에 담고, 각 영역에서 여러 다른 엣지 방향에 대해 히스토그램을 계산한다. 세 번째로, 단어 가방 feature 표현이 있다. 자연어 처리에서 단어 빈도를 세는 것과 유사한 개념이다. 이미지를 랜덤으로 잘라 샘플링하고, 클러스터링해서, 이미지 내의 시각적 단어(색깔이나 엣지)를 표현하는 클러스터를 만든다. 즉 첫 번째와 두 번째 방법을 어느정도 통합하고 있다고 보면 되겠다.
역전파 (Backpropagation)
신경망의 발전 역사를 살펴보자.




Frank roesnblatt(1957): 마크 원 퍼셉트론 머신 개발(최초의 퍼셉트론 머신, 0 or 1의 결과, 역전파 X)
Widrow and hoff(1960): Adaline과 madaline 개발(다계층 퍼셉트론 머신, 역전파 X 훈련 원칙 X)
Rumerhart(1986): 역전파 최초 도입
역전파는 출력층에서 시작해서 입력층으로 역으로 값을 전파해주는 과정인데, 이때 출력층을 초기 변수에 대해 미분하기는 어렵지만 바로 전 노드에 대해 미분하기는 쉬우므로 chain rule을 사용해서 계산한다.
Geoffrey E Hinton(2012): 합성곱 신경망을 처음 도입해서 ImageNet 분류 시 좋은 성능 보여줌.
CNN (convolutional neural network, 합성곱 신경망)

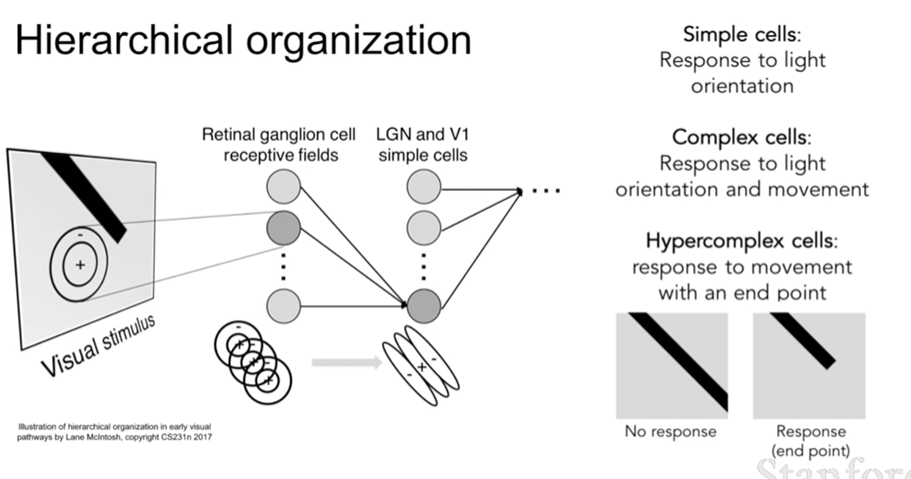
그렇다면 CNN은 무엇인가? CNN은 동물의 시각 피질의 뉴런의 작동 방식을 모방한다. 1950년대에 행해진 Hubble과 Wiesel의 실험에서 크게 두 가지 주요한 정보를 얻을 수 있는데, 시각 피질에서 인접 세포끼리 mapping 되어있다는 것과, 뉴런이 계층적인 구조(simple cells->complex cells->hypercomplex cells)를 가지고 있다는 것이다.

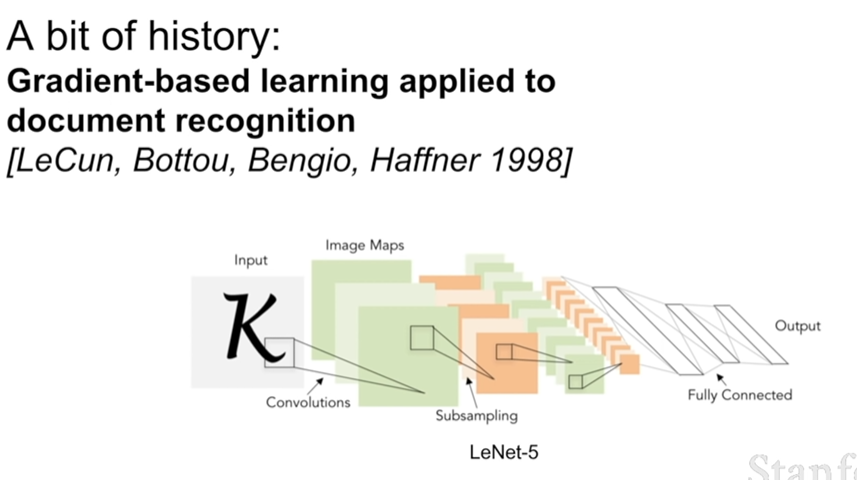


이 정보를 바탕으로 1980년 처음으로 neocognitron이라는 simple celss와 complex cells를 모방한 architecher가 제작되었다. 1998년 LeCun이 합성곱 신경망을 훈련시켜 우편번호 숫자를 성공적으로 인식할 수 있게 만들었다. 이미지 분류에 합성곱 신경망을 적용시키는 것은 이미지 데이터가 만연하고 컴퓨팅 기술이 많이 좋아진 2012년에서야 AlexNet에서 나타났다. 합성곱 신경망을 이용한 이미지 분류는 오늘날 많은 분야에서 사용된다.




합성곱 신경망은 어떻게 동작할까? 이미지를 길게 늘어뜨려 W와 내적하는 FC Layer와 다르게, CNN은 공간 구조를 유지하며 연산한다. 이미지 위로 필터가 정해진 칸 수(stride)씩 이동하며 겹쳐진 자리의 원소들끼리의 곱을 모두 더해, 내적하는 것이다. 이때 필터의 channel은 이미지의 channel과 동일하다. 한 번의 convolution을 마치면 1 channel을 갖는 하나의 feature map이 생긴다. 다른 필터로 동일한 과정을 거치면 또 하나의 1 channel feature map이 생긴다. Output의 channel 수는 필터의 개수로 조절할 수 있는 것이다. 또한 feature map의 크기는 (N-F)/stride+1 의 공식으로 구할 수 있다.(N: 입력 이미지 크기, F: 필터 크기) F는 양수이기 때문에 convolution을 수행할수록 출력 크기는 계속 작아질 수 밖에 없는데, 너무 빠르게 크기가 줄어드는 것을 방지하게 위해 입력 이미지의 외곽을 0으로 둘러싸는 zero padding을 진행할 수 있다. 이를 기반으로 1x1 convolution의 기능을 생각해볼 수 있는데, stride=1일 때 출력 이미지의 크기는 입력 이미지의 크기와 동일하면서, convolution 횟수를 조정해서 원하는 만큼의 channel을 가진 출력을 얻을 수 있다. 즉 입력 이미지의 크기를 건드리지 않으면서 channel을 줄일 수 있다. 이는 정보의 소실이 비교적 적으면서도 연산량을 줄일 수 있는 방법이다.



ConvNet에서는 합성곱 계층 사이사이에 pooling, 활성 함수 등을 배치한다. 마지막에는 FC layer를 거치게 된다. 결과는 우측과 같은데, 낮은 수준의 feature에서 높은 수준의 feature까지 얻어내는 계층 구조가 드러남을 알 수 있다. 이는 앞선 시각 피질의 계층적 특성과 동일하다. 이는 시각 피질의 특성을 반영하려고 의도한 것이 아니라, 구조를 만들고 나니 같은 특성을 얻게 된 것이다.
Pooling

합성곱 계층 사이에 pooling을 배치한다고 했는데, pooling이 뭘까? 1x1 convolution과 정 반대의 기능을 가진다. channel은 그대로 유지하되 크기는 줄여 관리하기 쉽게 만드는 것. 즉 downsampling 하는 것이다. 이는 channel이 1인 feature map 한 장 한 장에 대해 진행한다. 크기를 줄이기 위해서는, 즉 정보 숫자는 줄이면서 집단 내의 필요한 정보를 계속 표현해내기 위해서는 평균값을 사용할 수도 있을 것이고, 최빈값을 사용할 수도 있을 것이고, 최댓값을 사용할 수도 있을 것이다. 그런데 뉴런의 활성화를 측정하는 것이 목표이기 때문에, 최댓값을 사용하는게 적절하다.(대강은 알겠는데 잘 모르겠음!! 뉴런 비유를 건너뛰어서 그런 것 같음.)
FC layer
마지막에 FC layer를 사용한다고 했는데, 넓이X높이X깊이를 가진 전 단계를 1차원으로 길게 늘인다. 예측에는 공간 정보가 필요 없기 때문에, 오히려 방해가 될 수 있기 때문에 예측이 좀 더 용이하도록 이 작업을 수행해주는 것이다.
활성화 함수(activation function)

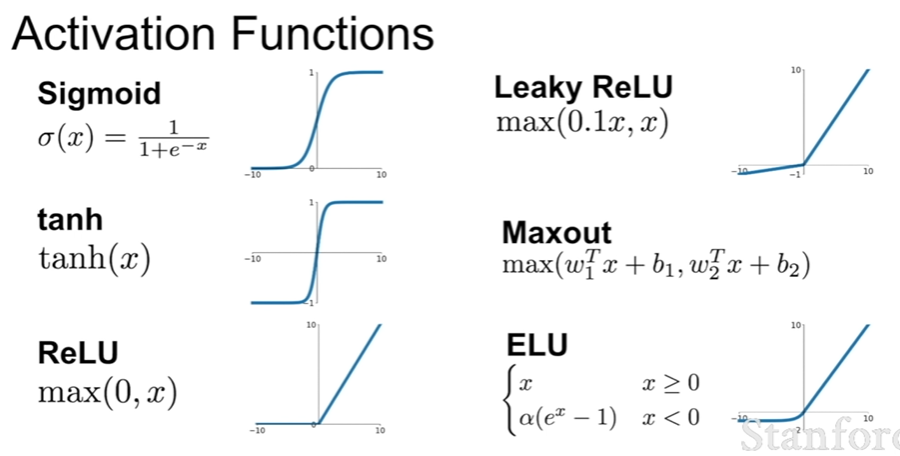
합성곱 신경망 사이에 또 활성화 함수를 배치한다고 했다. 활성화 함수는 또 뭘까? 생물 뇌의 뉴런은 자극을 입력으로 받아와서 자극이 역치 이상이면 활성화되어 출력하고 그렇지 않으면 출력하지 않는 것처럼, 입력 신호에 따라 출력 신호를 결정해주는(입력 신호를 약간 바꿔주는) 함수가 활성화 함수이다. 활성화 함수는 종류가 굉장히 많고, 각 그래프 개형에 따른 장단점도 뚜렷하다. 활성화 함수에서 대표적으로 발생할 수 있는 문제가 기울기 소실이다. Sigmoid나 tanh처럼 X가 +-무한대로 갈 때 기울기가 0에 수렴하면, 역전파 과정에서 기울기가 소실되는 것이다. 그러므로 양 극단에서 기울기가 0에 수렴하지 않으면 좋겠다. 또 다른 대표적인 문제는, 그래프의 치역이 오직 양수이거나 오직 음수이면 기울기가 오직 양수/음수 방향으로만 갱신된다는 것이다. 그러니 되도록이면 그래프의 중심이 (0,0)이어서 치역에 양수와 음수가 모두 포함되면 좋겠다. 그리고 exp() 함수는 계산 비용이 꽤 비싸니까 간단한 수식을 가진 함수면 좋겠다. 이 모든 조건을 만족시키지 못하는 sigmoid 함수는 좋은 활성화 함수가 아닐 것이다. 그러므로 실제 학습에서는 사용하지 않는다. Tanh는 하나의 조건을 만족시킨다. 쓸 수는 있으나 좋은 성능을 기대하기는 어렵다. 2개의 조건을 만족시키는 ReLU는 꽤 괜찮아보이지만 입력값이 음수일 때 아예 기울기가 갱신되지 않는다는 dead ReLU 문제가 발생한다. 이를 해결하기 위해 Leaky ReLU나 ELU를 쓸 수 있겠다. (맥스아웃은 설명할만큼 충분히 이해하지 못한 것 같다.) 일반적으로는 ReLU를 사용하며 학습률을 조정한다.
데이터 전처리
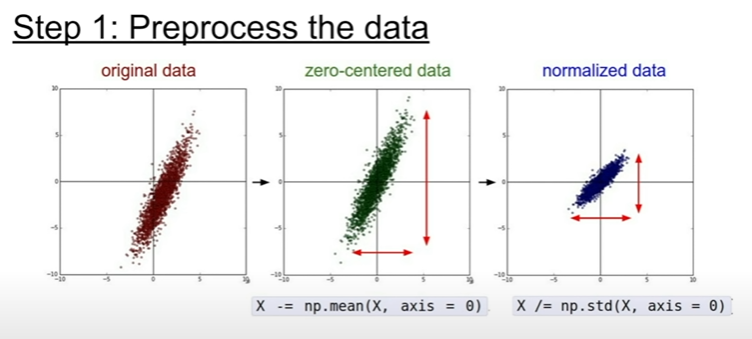
활성화 함수에서 중심이 (0,0)인 함수를 선호했던 것처럼, 데이터의 평균을 0으로 맞춰줄 수 있다. 정규화 할 수도 있으나(편차를 1로 만드는 걸까?) 이미지는 상대적으로 비교 가능한 크기와 분포를 가지기 때문에 정규화할 필요성이 크지 않다. 채널에 대해 평균을 맟주더라도 전체 이미지에 걸쳐 보면 크게 차이는 없다.
가중치 초기화

가중치를 갱신하려면, 시작값을 정해줘야한다. 깔끔하게 모든 파라미터에서 가중치를 0으로 설정하고 시작하면, 아니면 다른 어떤 값을 모든 파라미터에 적용시키면 모든 뉴런이 똑같이 학습될 것이다. 이를 해결하기 위해 분포에서 샘플링 가능한 작은 랜덤 숫자로 가중치를 설정할 수 있는데, 깊은 망에서 표준편차가 0으로 빠르게 다가간다. 결국에는 모든 뉴런이 +1/-1이 되어버리고, 모든 경사가 0이 되는 것이다. 좋은 가중치 초기화 방법으로는, Xavier initialization(ReLU와는 궁합이 좋지 않음)이나 He initialization이 있다.
Batch nomarlization


FC layer나 Convolution 이후 생긴 scaling 영향을 되돌리기 위해 배치 정규화를 한다. 현재 배치의 평균과 분산을 계산해서 이를 유지하도록 만드는 것이다.
'강의 & 책 > CS231N' 카테고리의 다른 글
| [CS231N] Lecture 15, 16 (0) | 2023.03.12 |
|---|---|
| [CS231n] Training Neural Networks II, Deep Learning Software (0) | 2022.05.01 |

