| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | ||||
| 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 11 | 12 | 13 | 14 | 15 | 16 | 17 |
| 18 | 19 | 20 | 21 | 22 | 23 | 24 |
| 25 | 26 | 27 | 28 | 29 | 30 | 31 |
- YAI 11기
- cl
- 강화학습
- cv
- YAI 10기
- YAI 8기
- RCNN
- YAI 9기
- Faster RCNN
- NLP #자연어 처리 #CS224N #연세대학교 인공지능학회
- rl
- NLP
- nerf
- 컴퓨터비전
- Perception 강의
- YAI
- 3D
- CS224N
- CS231n
- transformer
- GaN
- 연세대학교 인공지능학회
- Googlenet
- CNN
- PytorchZeroToAll
- 컴퓨터 비전
- VIT
- Fast RCNN
- GAN #StyleCLIP #YAI 11기 #연세대학교 인공지능학회
- 자연어처리
- Today
- Total
연세대 인공지능학회 YAI
[CS231n] Training Neural Networks II, Deep Learning Software 본문
Training Neural Networks II, Deep Learning Software
* YAI 9기 박찬혁 님이 심화 팀에서 작성한 글입니다.
Lecture 7 : Training Neural Networks II
Optimization
SGD
6강에서 배치단위로 Gradient Descent를 진행하는 SGD라는 Optimizer를 소개했다. SGD의 식은 아래와 같다.
$$
x_{t+1}=x_t-\alpha\nabla f(x_t)
$$
하지만 SGD에는 단점이 있는데 아래 그림처럼 현재 지점에서의 기울기만 보고 지그재그로 찾아간다는 점이다. 이렇게 진행을 하게되면 바로 최적점을 찾아가는 것 보다 훨씬 느리게 학습이 진행된다.

또한 이렇게 현재 지점에서의 기울기만 보고 이동지점을 판단한다면 Local minima나 saddle point에서는 기울기가 0인 지점이 있기 때문에 이동을 멈추게 된다. 하지만 위 두 점의 경우는 모델이 학습해야하는 최적점이 아니기 때문에 학습에 실패하게 된다. 특히 높은 차원을 가지는 모델에서는 안장점 문제가 자주 발생한다.
SGD는 전체 데이터가 아닌 배치를 가지고 기울기를 구하고 학습을 진행하기 때문에 노이즈가 많이 발생하여 비효율적인 학습을 진행한다.
따라서 이를 개선하기 위해 다른 Optimizer들이 개발된다.
Momentum
모멘텀 방식은 SGD에 관성의 개념을 입힌 Optimizer이다. 식은 아래와 같다.
$$
x_{t}=x_{t-1}-\alpha v_{t}
$$
$$
v_{t}=\rho v_{t-1}-\alpha\nabla f(x_t)
$$
위 식에서 $\rho$는 마찰계수와 같은 역할로 가중치의 흐름에 마찰을 준다. 보통 0.9~0.99의 값을 준다고 한다. 식의 $v$로 인해 이전에 움직인 속도를 저장하였다가 사용함으로써 움직였던 속도를 유지할 수 있게 해준다. 따라서 만약 local minima나 saddle point에 빠졌더라도 속도를 잃지 않고 빠져나갈 수 있게 해준다. 만약 속도 때문에 최적값을 지나가게 되었더라도 결국엔 돌아오는 모습을 보인다.
기존 momentum의 이동 방식은 아래의 왼쪽그림과 같다.

오른쪽의 Nesterov Momentum같은 경우는 일반 모멘텀 방식과는 다르게 현재 위치에서 기울기를 구하는 것이 아닌 현재 상태에서 관성으로 인해 가지고있는 속도로 진행한 곳에서의 기울기를 미리 계산해 다음 step에서 갈곳을 정하게 된다. 미리 다음 이동할 곳에서의 기울기를 구한다는 점에서 불필요한 이동을 최대한 줄이고자하는 효과를 얻을 수 있다. 하지만 이 방식은 Local minima가 없는 Convex function에서는 성능이 뛰어나지만 그 외의 함수에 대해서는 일반 모멘텀과 성능이 크게 다르지 않다. 게다가 거의 대부분의 상황이 non-convex function이기 때문에 계산이 모멘텀보다 복잡한 Nesterov Momentum은 인공 신경망 모델에서는 많이 사용되지 않는다.
Adagrad(Adaptive Gradient)
Adagrad의 아이디어는 입력변수가 둘 이상일때 각각의 파라미터에 변화의 정도를 다르게 하여 업데이트를 진행하는 것이다. 이름에서 볼 수 있듯이 ‘적응적’으로 학습률을 조절하는 방식이다. 계속해서 업데이트가 된 변수는 최적값에 가까워졌을 확률이 높으니 업데이트 되는 정도(step size)를 줄이고, 업데이트가 거의 되지 않은 변수는 업데이트 되는 정도를 크게하여 효율적으로 최적값을 찾게한다.
$$
h_t = h_{t-1}+\frac{\sigma L}{\sigma \omega} \cdot \frac{\sigma L}{\sigma \omega}
$$
$$
\omega_t = \omega_{t-1} - \alpha \frac{1}{\sqrt{h_t}}\frac{\sigma L}{\sigma \omega}
$$
위 식에서 볼 수 있듯이 현재 위치의 기울기에 $\frac{1}{\sqrt{h}}$가 곱해져서 업데이트가 된다. 하지만 $h$는 기울기의 제곱이라는 항상 양수인 값이 더해지기 때문에 항상 양수이고, 계속해서 커지는 것을 볼 수 있다. $h$가 계속 커진다면 결국에는 기울기에 너무 작은 값이 곱해져 거의 학습이 안되는 순간이 올 수 있다. 이 방식도 Convex한 경우에는 바로 최적점을 찾아갈 수 있지만 그 밖에는 도중에 멈출 수 있는 위험이 있다.
이에 대한 대안으로 나온 방법이 RMSProp이다.
RMSProp
RMSProp에서는 Adagrad의 h 계산 식이 아래와 같이 바뀌었다.
$$
h = \rho h + (1-\rho)\frac{\sigma L}{\sigma \omega} \cdot \frac{\sigma L}{\sigma \omega}
$$
$\rho$는 decay_rate로 h가 업데이트 될 때 이전 h값과 기울기가 반영될 비율을 정할 수 있게 되었다. 이전 h값이 지금까지의 모든 기울기값의 합이기 때문에 이는 최신 기울기값이 얼마나 반영되게 할 것인지 결정할 수 있게 되었다는 의미이기도 하다.
Adam(Adaptive Moment Estimation)
위의 RMSProp과 Momentum기법을 합친 optimizer이다. 모멘텀의 관성 개념과 Adagrad에서 나온 ‘적응’에 대한 개념이 합쳐졌다. RMSProp의 h와 momentum의 v값을 모두 사용하여 step size를 조절하는 h의 특성과 momentum의 관성 특성을 모두 가졌다.
$$
v_t = \gamma v_{t-1} - (1-\gamma) \frac{\sigma L}{\sigma \omega}
$$
$$
h_t = \rho h_{t-1} + (1-\rho)\frac{\sigma L}{\sigma \omega} \cdot \frac{\sigma L}{\sigma \omega}
$$
$$
\omega_t = \omega_{t-1} - \frac{v_t}{\sqrt{h_t + \epsilon}}
$$
$\epsilon$은 분모에 0이 곱해지지 않게 하기 위한 작은 값이다. $\rho=0.999, \gamma=0.9$ 정도의 값이 추천된다.
하지만 여기서 첫번째나 step을 진행할 때 맨 처음의 $v_t$와 $h_t$는 0이기 때문에 첫 이동량이 엄청 크게 나올 수 있다. 따라서 최종 식을 아래와 같이 바꿨다.
$$
\omega_t = \omega_{t-1} - \frac{\frac{v_t}{1-\gamma^t}}{\sqrt{\frac{h_t}{1-\rho^t} + \epsilon}}
$$
보면 v,h에 $1-\rho^t$와 $1-\gamma^t$를 나눠줌으로써 초반에 값이 튀지 않도록 보정해준다.
위와 같은 여러 Optimizer들을 사용하다 보면 Learning rate를 설정하는 것도 학습에 큰 영향을 미친다는 것을 알 수 있다. 강의에서는 이 learning rate를 설정하는 방법으로 learning rate decay를 소개했다. 이 방법은 시간이 지날수록 learning rate를 낮춰가면서 실험을 진행한다.
$$
\alpha=\alpha_0e^{-kt} or \alpha = \frac{\alpha_0}{(1+kt)}
$$
주로 위 식과 같은 방법으로 k를 조절하며 진행하게 된다.
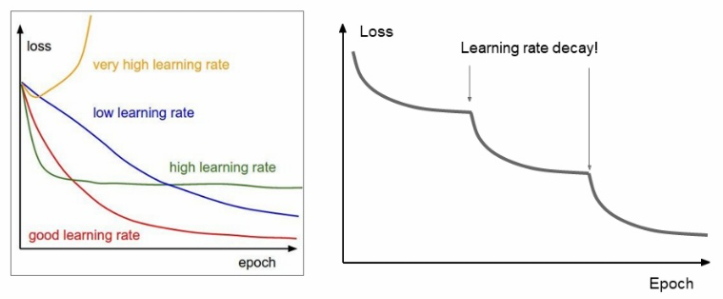
위 방법을 실행할 시 그래프가 위 모습처럼 나오게 되는데 이는 learning rate가 너무 커서 깊은곳으로 들어가지 못하다가 learning rate를 낮추면서 더 적절한 지점으로 찾아들어가는 것으로 이해할 수 있다.
Second-order Optimization
지금까지의 가중치 갱신은 모두 아래의 그림과 같이 한 점에서의 기울기를 구하여 갱신을 진행했다.
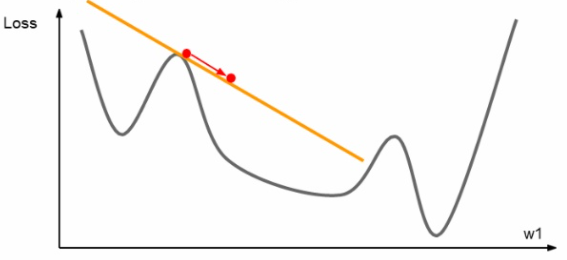
하지만 위와 같이 직선을 이용한 진행 말고도 해당 점의 기울기에서 파생된 곡선을 이용한 갱신도 고려해 볼 수 있다. 해당 점에서 2차 테일러 근사 함수를 구해 해당 그래프와 유사한 2차 곡선을 구하여 아래 그림과 같이 갱신을 진행할 수 있다.
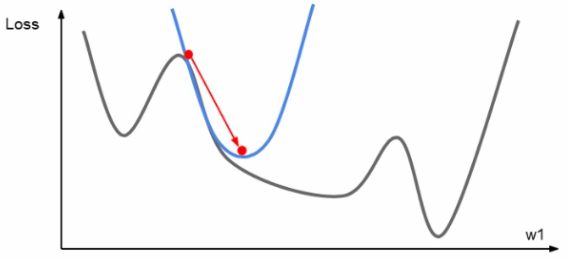
Second-order optimization의 장점은 first-order와는 다르게 learning rate가 필요하지 않다는 점이다. 해담 점에서 이차 테일러 근사함수를 구하면 그 함수의 최솟값은 바로 계산하여 나올 수가 있기 때문에 바로 다음 step을 찾아갈 수 있다. 그래서 first-order보다 더 빠르게 최솟값을 찾아갈 수 있다는 장점이 있지만 큰 단점이 존재한다.
$$
J(\theta)\approx J(\theta_0) + (\theta - \theta_0)^T\nabla_\theta J(\theta_0)+\frac{1}{2}(\theta-\theta_0)^T\bf H(\theta-\theta_0)
$$
$$
\theta^* = \theta_0-\bf H^{-1}\nabla_\theta J(\theta_0)
$$
2차 테일러 근사함수를 구하고 뉴턴 방법을 통해 업데이트를 진행하는 위 식을 보면 Hessian matrix를 구하고 그 역수를 취해 계산에 사용한다. Hessian matrix는 만약 모델의 parameter가 n개라면 $n\times n$의 크기를 가지는 행렬이다. 일단 이 행렬을 구하는데도 $O(N^2)$의 시간 복잡도가 들게되고, 이 행렬의 역수를 구하는 것 까지 시행하면 $O(N^3)$의 시간 복잡도를 띄게되어 연산 시간이 엄청나고, 메모리도 많이 소모되게 된다.
따라서 Quasi-Newton 방법같이 Hessian matrix를 근사하며 시간복잡도를 줄이는 방법도 있고, Hessian matrix를 nxn으로 전부 저장하지 않고 갱신하면서 사용하는 방법인 L-BFGS도 있다. 이 방법들은 하나의 convex 함수만 가지고 계산할 수 있는 모델이라면 잘 작동하지만 전체 데이터셋을 한번에 사용해야지만 잘 작동하고 mini-batch를 사용할 때는 좋은 결과를 내지 못한다는 단점이 있다.
Ensembles models
지금까지 해왔던 방법들은 모두 Trainset의 정확도를 높이는 방법이였다. 이렇게 하면 Train set과 Test set의 성능 차이가 생기는 overfitting이 생길 수 있는데 이를 해결하기위해 고안된 방법이 앙상블 모델을 활용하는 방법이다.
앙상블 모델은 여러 모델을 학습시켜 그 평균값을 실제 Test에 사용하는 방법이다. 하지만 여러 모델을 만들어서 학습시키면 해야할 것이 많기 때문에 한 모델을 학습시키면서 중간중간 snapshot을 찍는 방법으로 모델 학습을 여러구간으로 나눠 일정 반복 횟수마다 새로 학습을 진행하여 마지막에 합침으로써 앙상블 효과를 낸다. 또한 일정 구간마다 learning rate크게 바꾸며 진행하는것도 학습에 좋은 영향을 미친다는 결과도 있다.
Regularization
앞에서 배운 Regularization은 아래와 같은 Term을 loss function에 추가하는 것이였다.
$$ \text{L2 regularization} \quad \quad R(W) = \sum_k \sum_l W^2_{k,l} $$
$$ \text{L1 regularization} \quad \quad R(W) = \sum_k \sum_l \lvert W_{k,l} \rvert $$
$$ \text{Elastic net(L1 + L2)} \quad \quad R(W) = \sum_k \sum_l \beta W^2_{k,l} + \lvert W_{k,l} \rvert $$
하지만 실제 Neural Network에서는 이와같은 방법을 많이 사용하지는 않는다. 그 대신 자주 사용하는 방법이 Dropout이라는 방법이다.
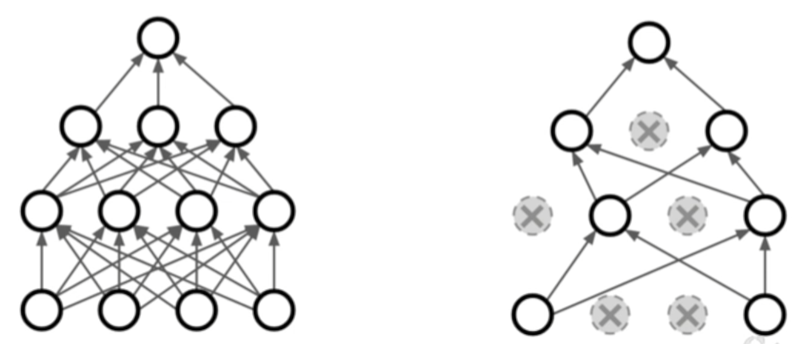
Dropout은 말 그대로 일부 뉴런들을 ‘떨어뜨리는’ 방법으로 사용자가 정한 일정 비율로 뉴런의 가중치값을 0으로 만들어 연산에 관여하지 못하게 만드는 방법이다. 보통 그 비율은 0.5로 설정한다.
Dropout 방법을 사용하게 되면 학습이 진행될 때 관여하는 뉴런이 계속 달리지게 되기 때문에 여러 모델을 앙상블하는 효과를 보이게 된다. 따라서 Overfitting을 막을 수 있게 되는 것이다.
이미지를 인식할 때 각 뉴런은 특정한 이미지의 특성에 대해 관찰하는 역할을 한다. 학습을 진행하게 될수록 이 특성에 대해 더 잘 학습하게 되는데 만약 뉴런이 한가지 특성만 보고 대상을 판별하게 된다면 overfitting될 가능성이 높아지는 것이다. 하지만 dropout을 통해 특정 특성만 바라보는 뉴런을 끄게된다면 다른 뉴런이 그 특성까지 고려해야하기 때문에 한 뉴런이 다양한 특성을 보게되는 효과를 볼 수 있다.
Dropout은 Train에서만 사용하고, Test에서는 사용하지 않는다. Test에서 사용하기 위해 온전한 모델을 뽑아내야하는데 Dropout이 확률로 진행된 과정이기 때문에 그 평균값을 구하려면 Train에서 나온 모델에 확률을 곱하여 적분하는 과정이 필요하다. 하지만 이 과정은 연산을 많이 잡아먹기 때문에 좀 더 간단화된 방법을 많이 사용한다.
$$\text{At test time we have: } E[a] = w_1x + w_2y$$
$$\text{During training we have: } $$
$$E[a] = \frac14 (w_1x + w2_y) + \frac14 (w_1x + 0_y) + \frac14 (0x + 0_y) + \frac14 (0x + w2_y) = \frac12 (w_1x + w2_y) $$
위 식과 같이 만약 $w_1x+w_2y$라는 단순한 신경망이 있을 때 0.5의 Dropout을 적용한다면 위 식과 같이 결과가 기존 모델에 0.5를 곱한 값이 나오게 된다. 따라서 큰 모델을 사용할 때도 최종 결과에 Dropout의 비율을 곱해주면 적분하여 구한 값과 유사하게 나온다.
하지만 Test에서는 보통 모델에 입력을 넣어 출력을 받기 때문에 연산이 없을수록 좋다. 따라서 출력에 dropout 비율을 곱해주는 대신에 Train에서 dropout 비율의 역수를 곱해 연산을 진행하는 것으로 같은 효과를 얻을 수 있다.
Dropout은 모델을 일반화시키는 방법 중 하나로 너무 Train set에 fit하게 학습되는 것을 피하게 해주는 방법 중에 하나이다. 이와 비슷한 방법으로 Batch Nomalization도 비슷한 효과를 거둘 수 있다.
또 다른 방법으로는 Data Augmentation이 있다. Data Augmentation은 입력되는 이미지를 뒤집고, 일부를 잘라내고, 노이즈를 조금씩 주는 등의 변형을 가해 학습을 진행하게 된다. Data augmentation을 통해 학습을 진행시키게 되면 제한된 이미지의 개수로 계속 이미지를 바꿔주면서 학습을 진행할 수 있고, 학습데이터가 늘어난 효과를 줌으로써 overfitting을 방지할 수 있다.
Dropout과 비슷한 방법으로는 Dropconnect가 있다. dropout은 임의의 뉴런을 커서 그 뉴런에서 다음 뉴런으로 넘어가는 모든 값을 0므로 바꾸었지만 dropconnect는 뉴런의 값은 그대로 두되 뉴런에서 뉴런으로 넘어가는 길을 임의로 막는 방법이다. 이 방법은 단순히 뉴런을 막는 것 보다 더 많은 경우의 수가 있어서 대체적으로 조금 더 좋은 결과를 낸다고 한다.
Fractional max pooling이라는 방법은 Pooling을 기존처럼 2*2칸씩 일정하게 자르는게 아닌 아래의 그림처럼 무작위로 지역을 선정하여 pooling하는 방법이다.

이 방법 또한 Test에서 같은 방식을 사용할 순 없기 때문에 pooling의 평균값을 취하거나 일반적인 2*2 pooling을 사용하기도 한다.
Stochastic depth는 dropout처럼 뉴런들을 끄는게 아닌 레이어 자체를 무작위로 끄면서 학습하는 방법으로 효과 자체는 dropout과 비슷하다고 한다.
Transfer Learning
Transfer learning은 전이학습으로 기존에 학습되어있는 모델을 가져와서 우리가 가지고있는 데이터셋에 적용하는것을 말한다.
ImageNet과 같이 많은 데이터셋과 많은 class를 갖고있는 매우 큰 데이터셋으로 학습된 모델을 들고와서 맨 마지막의 FC레이어만 초기화를 시켜 사용한다. 마지막 레이어만 초기화시키는 이유는 학습된 모델이 입력 이미지의 특성을 뽑아내는 능력은 그대로 사용하되 그 특성을 클래스와 짝짓는 기능만 우리가 필요한 식으로 바꿔서 사용하면 되기 때문이다.
이때 우리가 가지고있는 데이터셋의 특징에 따라 사용하는 방법이 조금씩 다른데 아래의 표를 따른다.
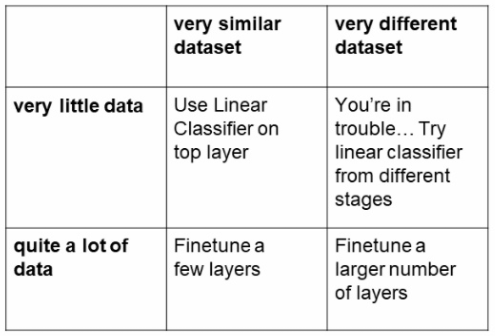
우리가 가지고있는 데이터셋이 우리가 전이학습에 사용할 모델이 학습한 데이터셋과 얼마나 비슷한지, 그리고 우리가 가지고있는 데이터셋이 얼마나 많은지에 따라 달라진다.
CNN같은 경우 우리가 가진 데이터셋이 작고 이미 학습된 데이터셋과 비슷하다면 제일 마지막 FC레이어만 초기화하여 학습을 시키면 좋은 결과를 얻을 수 있다. 우리의 데이터셋이 큰데 기존 데이터셋과 클래스가 비슷하다면 마지막 레이어보다 조금 더 올라간 몇몇의 레이어들을 제외한 레이어들만 프리징 시키고 학습을 진행하면 된다. 이때 가중치들을 크게 바꿀 필요는 없기 때문에 learning rate를 낮춰서 조금씩만 학습시키는 방법으로 간다.
하지만 우리의 데이터셋이 기존의 데이터셋과는 전혀 다른 유형의 데이터라면 좀 더 많은 레이어들을 초기화시켜서 다시 학습을 진행해야할 것이다. 이때도 데이터셋의 개수가 적다면 큰 효과를 보지 못할수도 있다. 하지만 데이터셋이 많다면 새로운 모델을 학습시키는 것 보다는 좋은 효과를 볼 수 있다.
Lecture 8 : Deep Learning Software
CPU vs GPU
컴퓨터 부품인 CPU와 GPU는 서로 다른 특성을 가지고 있다.
CPU(Central Processing Unit)
- 코어의 수는 적지만 Clock speed가 빠르다.
→ 순차적 계산에 좋다. - 임시 저장소인 cache가 있지만 자체 메모리는 없어서 컴퓨터의 메모리를 공유한다.
- 복잡한 식을 빨리 계산하는데에 유리하다.
ex) 큰 수 몇개의 팩토리얼을 구하는데는 순차적계산이 필요하기 때문에 CPU가 유리하다.
GPU(Graphics Precessing Unit)
- Clock speed가 CPU보다는 낮지만 코어의 수가 몇백개에서 몇천개로 매우 많다.
→ 병렬계산에 특화되어있다. - 자체 메모리를 가지고 있다.
- 많은 수의 단순한 계산을 하는데 유리하다.
ex) 큰 행렬의 더하기 연산을 할 때 GPU가 유리하다. - 최근에 나온 GeForce RTX 3090같은 경우 코어가 10496개
GPU는 CUDA를 사용하여 쓸수있다.
학습에 GPU를 사용할 때는 보통 모델과 모델의 가중치를 GPU에 올려놓는다. 하지만 데이터셋같은 경우는 처음엔 컴퓨터 메모리에 있기 때문에 GPU에서 연산을 진행하기 위해서는 컴퓨터 메모리에서 GPU메모리로 옮기는 작업이 반복적으로 일어난다. 따라서 데이터를 옮기는 속도가 학습 속도에도 큰 영향을 준다. 이를 향상시키는 방법들이 여러가지 있다.
- 데이터셋의 양이 많지 않다면 RAM에 데이터셋을 모두 올려놓기
- HDD 대신에 SDD를 사용하기
- 미리 데이터를 불러오기위해 CPU의 멀티쓰레딩 사용하기
Framework
딥러닝에서는 프레임 워크를 사용한다. 그 이유는 프레임 워크가 Gradient를 쉽게 계산할 수 있고, 그래프를 쉽게 그릴 수 있으며 GPU에 특화되어있다.
Computational graph
주로 딥러닝에 사용되는 프레임워크에는 Caffe, PyTorch, TensorFlow등이 있다.
만약 우리가 딥러닝에 numpy같은 라이브러리만 사용한다면 기울기같은 연산은 우리가 일일이 구해야 할 뿐 아니라 GPU의 활용을 할 수 없다. 하지만 TensorFlow나 PyTorch같은 프레임워크들은 자동으로 계산해주는 기능들이 있다.
딥러닝 프레임워크의 대표격인 TensorFlow와 PyTorch는 차이가 있다. TensorFlow는 Static graph 방식으로 처음에 구현한 Computational graph를 계속 재사용한다. 반면에 PyTorch는 Dynamic graph방식으로 매 iteration마다 Computation graph를 새로 생성하며 진행한다.
Static graph의 장점은 아래와 같다.
- 초기에는 Computational graph를 구성하느라 조금 느릴 수 있지만 계속 반복사용하기 때문에 학습을 진행할 수록 효율성이 좋아진다.
- 그래프의 자료구조를 별도의 파일형태로 저장이 가능해서 코드에 접근하지 않더라도 해당 저장 파일만 있으면 모델을 구동할 수 있다.
Dynamic graph의 장점은 아래와 같다.
- 코드면에서 간결하다.
- 모델 안에 조건이 들어가야하는 상황이라면 Dynamic graph는 쉽게 만들 수 있지만 Static graph는 별도의 함수를 사용해야하고 코드가 복잡해진다.
- 진행 상황을 알 수 있으며 진행중인 각 계산에 접근이 가능하다.
위에서 소개한 프레임워크중 Tensorflow는 구글에서 만들었고, 자체적으로 연구와 배포가 가능하다. Pytorch같은 경우는 Facebook에서 만들었고, 연구에 특화되어있다. 그래서 Caffe2가 배포의 역할을 담당하고 있다. Caffe2같은 경우 모바일에서 잘 작동할 수 있도록 만들어져있다. 하지만 PyTorch같은 경우도 PyTorch Live, TorchServe와 같은 배포용 라이브러리도 있다.
'강의 & 책 > CS231N' 카테고리의 다른 글
| [CS231N] Lecture 15, 16 (0) | 2023.03.12 |
|---|---|
| [CS231N] DNN 기초 (0) | 2023.01.14 |

