| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | ||
| 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 13 | 14 | 15 | 16 | 17 | 18 | 19 |
| 20 | 21 | 22 | 23 | 24 | 25 | 26 |
| 27 | 28 | 29 | 30 |
- YAI 10기
- CS224N
- Fast RCNN
- YAI 8기
- 컴퓨터 비전
- CS231n
- 3D
- Perception 강의
- transformer
- RCNN
- rl
- NLP
- YAI 9기
- nerf
- Faster RCNN
- VIT
- GaN
- NLP #자연어 처리 #CS224N #연세대학교 인공지능학회
- YAI
- GAN #StyleCLIP #YAI 11기 #연세대학교 인공지능학회
- 연세대학교 인공지능학회
- PytorchZeroToAll
- Googlenet
- CNN
- cl
- 컴퓨터비전
- 자연어처리
- cv
- YAI 11기
- 강화학습
- Today
- Total
연세대 인공지능학회 YAI
[PytorchZeroToAll] Deep Learning Introduction 본문
YAI 11기 조믿음님이 기초부원팀에서 작성한 글입니다
Study Material
- PyTorchZeroToAll Lecture 1 ~ 11
- 모두를 위한 딥러닝 시즌 2 Lab 1 ~ 6
Index
- What is Machine Learning?
- Linear Model
- Linear Regression
- Gradient Descent
- Back Propagation
- Chain Rule Review
- Logistic Regression
- Binary Prediction
- Sigmoid Function
- Binary Cross Entropy Loss
- Softmax Classifier
- Softmax Function
- PyTorch Basics
- Discussion
What is Machine Learning/Deep Learning?
Machine learning is a branch of artificial intelligence(AI) that uses a group of algorithms that allows machines to learn from data without being programmed explicitly. Through iterative learning process, it can accurately predict or infer a reasonable output as the human brain can do — or even better. Among various methodologies of machine learning, deep learning is one approach in which neural networks are utilized.
Linear Model
Linear Regression
In linear regression problem, we need to find a linear relationship between an independent variable (i.e. $x$, hours of study, size of a house) and a dependent variable (i.e. $y$, gpa, price of a house).
For example, data below shows how the price of a house varies with its size.
| x(size) | y(price) |
|---|---|
| 1 | 3 |
| 2 | 6 |
| 3 | 9 |
By inspection, we know that the price is three times the size.
$y = 3*x$
Assume we have a machine that has one weight and no bias term.
$\hat{y} = x*w$ ( $\hat{y}$ denotes the predicted output )
We will use MSE(mean squared error) as our loss function to quantify how bad our machine is performing.
$loss = \dfrac{1}{N}\displaystyle\sum_{n=1}^{N}(\hat{y}_n-y_n)^2$
Since there is only one input data, the loss function can be simplifed as below:
$loss = \displaystyle(\hat{y}-y)^2=(x*w-y)^2$
Our goal is to find the value of weight $w$ that minimizes the value of the loss function. This can be achieved by computing the gradient of the loss function with respect to the weight and updating the value of the weight in every step of the learning cycle. We refer this process as backward pass.
Gradient Descent
$gradient = \dfrac{\partial{loss}}{\partial{w}}$
FYI, if the training data is randomly selected from the dataset and the machine uses gradient descent method, then it is called SGD(Stochastic Gradient Descent). When the training is based on computing the mean gradient of the entire training dataset, it is known as BGD(Batch Gradient Descent).
Update Mechanism
$w=w-\alpha\dfrac{\partial{loss}}{\partial{w}}$ ( $\alpha = \text{learning rate}$ )
Going back to our linear regression problem,
$loss=(\hat{y}-y)^2 = (x*w-y)^2$
$\dfrac{\partial{loss}}{\partial{w}}=2x(x*w-y)$
$\therefore w = w - \alpha\dfrac{\partial{loss}}{\partial{w}}=w-\alpha*2x(xw-y)$
Back Propagation
A typical neural network involves thousands or even millions of weights and biases. In this case, computing the gradient of each weight and bias is repetitive and time-consuming. Fortunately, there is a better and faster algorithm called back propagation. It is based on the chain rule. You don’t need to compute the gradient for values that are fixed(i.e. input x and label y).
Chain Rule Review
Let’s assume two functions below:
$f = f(g)$ and $g =g(x)$
The gradient is calculated by $\dfrac{\partial{f}}{\partial{x}}=\dfrac{\partial{f}}{\partial{g}}\dfrac{\partial{g}}{\partial{x}}$
Logistic Regression
Binary Prediction
In a binary prediction problem, the output has to be one of two classes(i.e. 0 or 1, yes or no, etc.). Referring back to the previous linear model, the machine can produce values greater than 1 or less than 0 depending on the weight $w$. Here, we will use an activation function called sigmoid function to limit the range of the output.
Sigmoid Function
$\sigma(x) = \dfrac{1}{1+e^{-x}}$
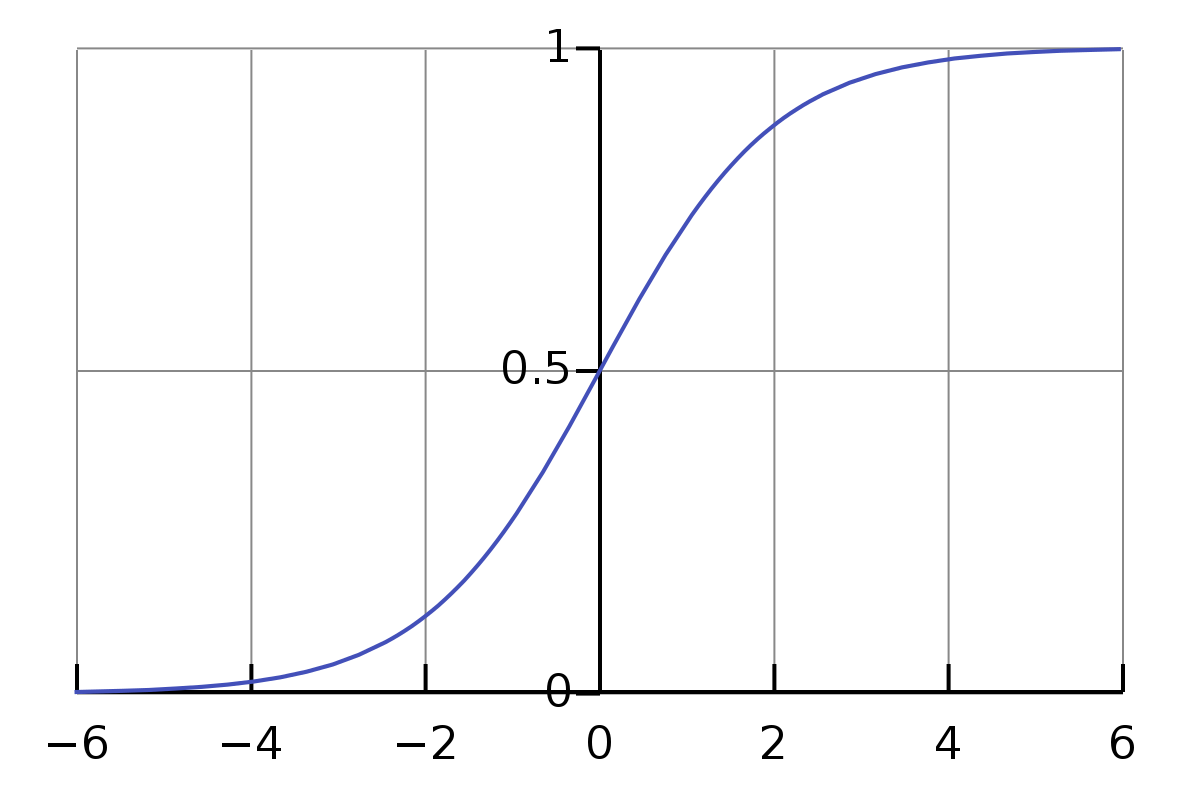
Binary Cross Entropy Loss(BCE Loss)
$loss = -\dfrac{1}{N}\displaystyle\sum_{n=1}^{N}y_nlog(\hat{y}_ n) + (1-y_n)log(1-\hat{y}_ n)$
Softmax Classifier
Multiple classes, multiple labels
In order to achieve this, two conditions need to be met:
- Output layer puts out the same number of values as the given classes
- Each output represents the probability of being labeled as the corresponding class → Softmax function
Softmax Function
$\sigma(bold{z})_ j=\dfrac{e^{z_j}}{\sum^{K}_ {k=1}e^{z_k}} \text{ for j = 1, ..., K where K is the number of classes}$
For a multiclass classifier, cross entropy loss is used as the loss function.
$loss = -\dfrac{1}{N}\sum^N_iy_ilog(\hat{y}_i)$
$y$ is the one-hot label vector where the element representing the correct class is set to 1 and the rest are set to 0 while $\hat{y}$ is the vector where each element represents the probability of the corresponding class being true.
nn.CrossEntropyLoss() includes both softmax and the cross entropy loss function
PyTorch Basics
Naming Convention
0D Scalar
1D Vector
2D Matrix
3D~ Tensor
.ndim() | .dim() - returns the number of dimensions of the tensor
Tensor Shape Convention
2D → $\text{(batch size, dim)}$
3D(CV) → $\text{(batch size, width, height)}$
3D(NLP) → $\text{(batch size, length, dim)}$
.shape | .size() - returns the size of the tensor
.size(dim=??) - returns the size of the given dimension of the tensor
Creating a Tensor with Specific Datatypes
torch.FloatTensor(seq) → Tensor of floating point numbers
torch.LongTensor(seq) → Tensor of integers
torch.ByteTensor(seq) → Tensor of booleans(1 or 0)
Basic Operations
torch.mul(a, b) - elementwise product(Hadamard product)
torch.mm(a, b) - matrix multiplication without broadcasting
torch.matmul(a, b) - matrix multiplication with broadcasting
.mean() — cannot be used on integers, must be of float da
.sum()
.max()
.argmax()
dim=? → explicitly set the dimension of which you are interested(this will be the dimension that is going to disappear)
For example, setting the argument dim=0 for a 2D matrix will going to produce a 1D vector as the final result.
.view(shape) - returns a new tensor with a different shape
.squeeze() - returns a new tensor with all the dimensions of size 1 removed
.unsqueeze(dim) - returns a new tensor with a dimension of size 1 inserted at the specified position
.ones_like()
.zeros_like()
.[function]_() — in-place operation(simply add an underscore at the end of the method)
i.e. .mul_() / .scatter_()
.scatter_(dim, index, src) - write all values from the tensor src into self at the indices specified in the index tensor
For a 3-D tensor,
self[index[i][j][k]][j][k] = src[i][j][k] # if dim == 0
self[i][index[i][j][k]][k] = src[i][j][k] # if dim == 1
self[i][j][index[i][j][k]] = src[i][j][k] # if dim == 2torch.Tensor.scatter_ - PyTorch 1.13 documentation
Discussion
- Why do sigmoid functions lead to gradient vanishing problem in deep neural networks?
- Sigmoid functions can lead to gradient vanshing problem if the layers become very deep. The derivative of the sigmoid function is calculated as $\sigma(z)*(1-\sigma(z))$ and the gradient of the loss with respect to the sigmoid layer is $\frac{\partial{loss}}{\partial{z}}=\frac{\partial{loss}}{\partial{a}}*\frac{\partial{a}}{\partial{z}}=\frac{\partial{loss}}{\partial{a}}*\sigma(z)*(1-\sigma(z))\text{ where } a = \sigma(z)$ . The range of the sigmoid function is always between 0 and 1 and hence, multiplying by the derivative of the sigmoid will cause the gradient to continuously decrease as the network undergoes backward pass.
- ReLU vs Sigmoid - Why is ReLU better as an activation function? What makes it more efficient during training?
- ReLU function definition: $f(x) = max(0,x)$
Derivative of ReLU: $f=\begin{cases}
0 &\text{if }(x<0) \
1 &\text{if }(x>0)
\end{cases}$
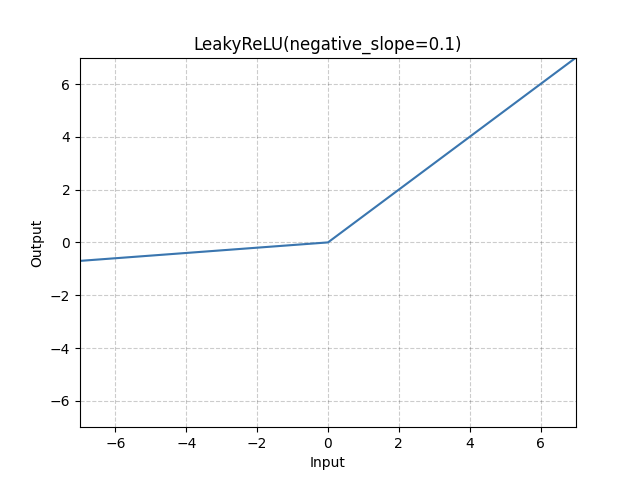
ReLU function can be one solution to the gradient vanishing problem of the sigmoid function. As you can see from above, the derivative of ReLU is either 0 or 1 depending on the value of $x$(note that it is not differentiable at x = 0). Unlike the sigmoid function, it does not multiply the gradient by a value between 0 and 1 and and a result, the gradient will not decrease. However, the gradient vanishing problem still remains due to the possibility of multiplying the gradient by 0(when x is negative). To overcome this, we can use LeakReLU where a gentle slope exists in $(x<0)$.
ReLU stands for Rectified Linear Unit.
ReLU
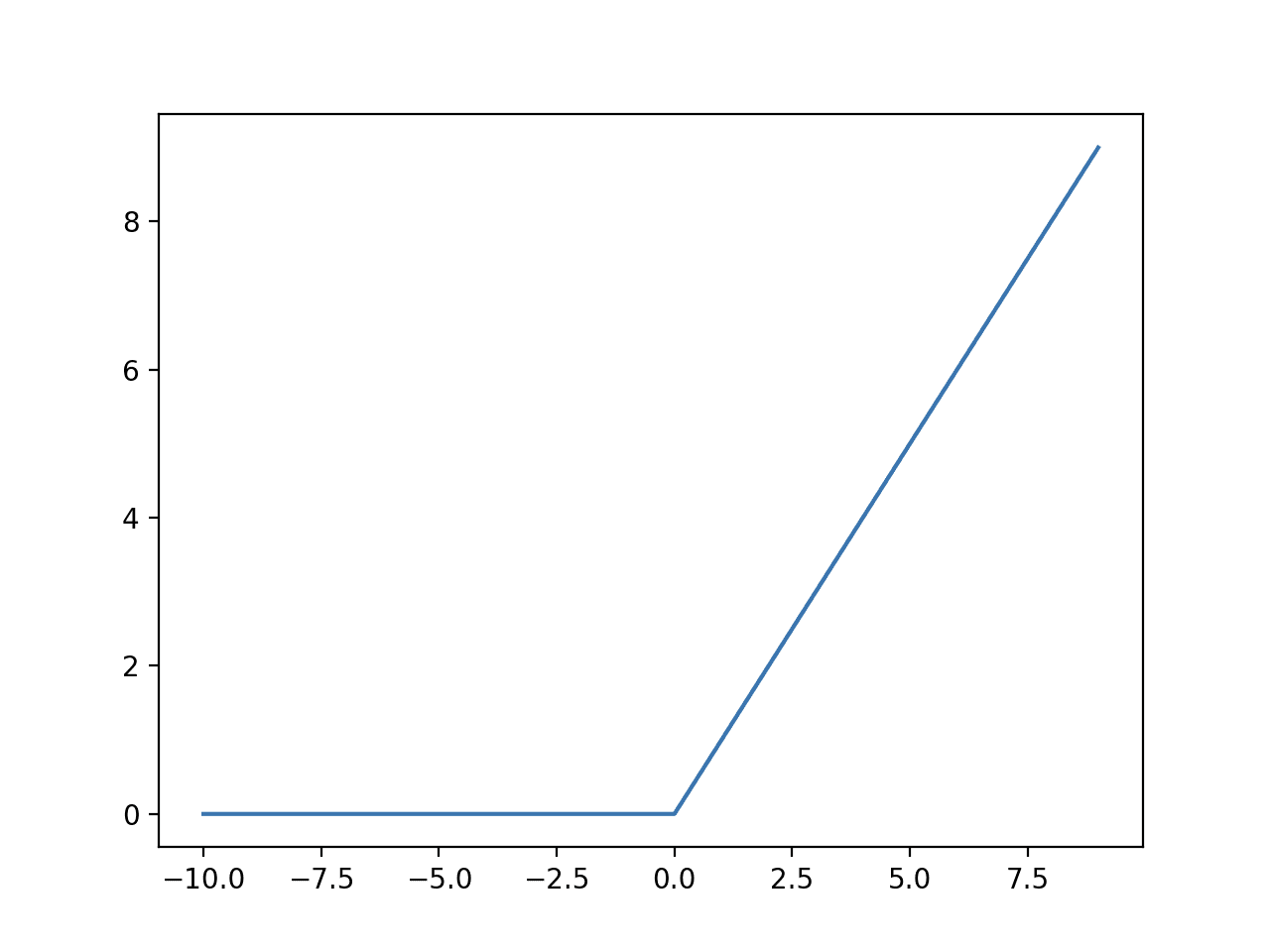
LeakyReLU
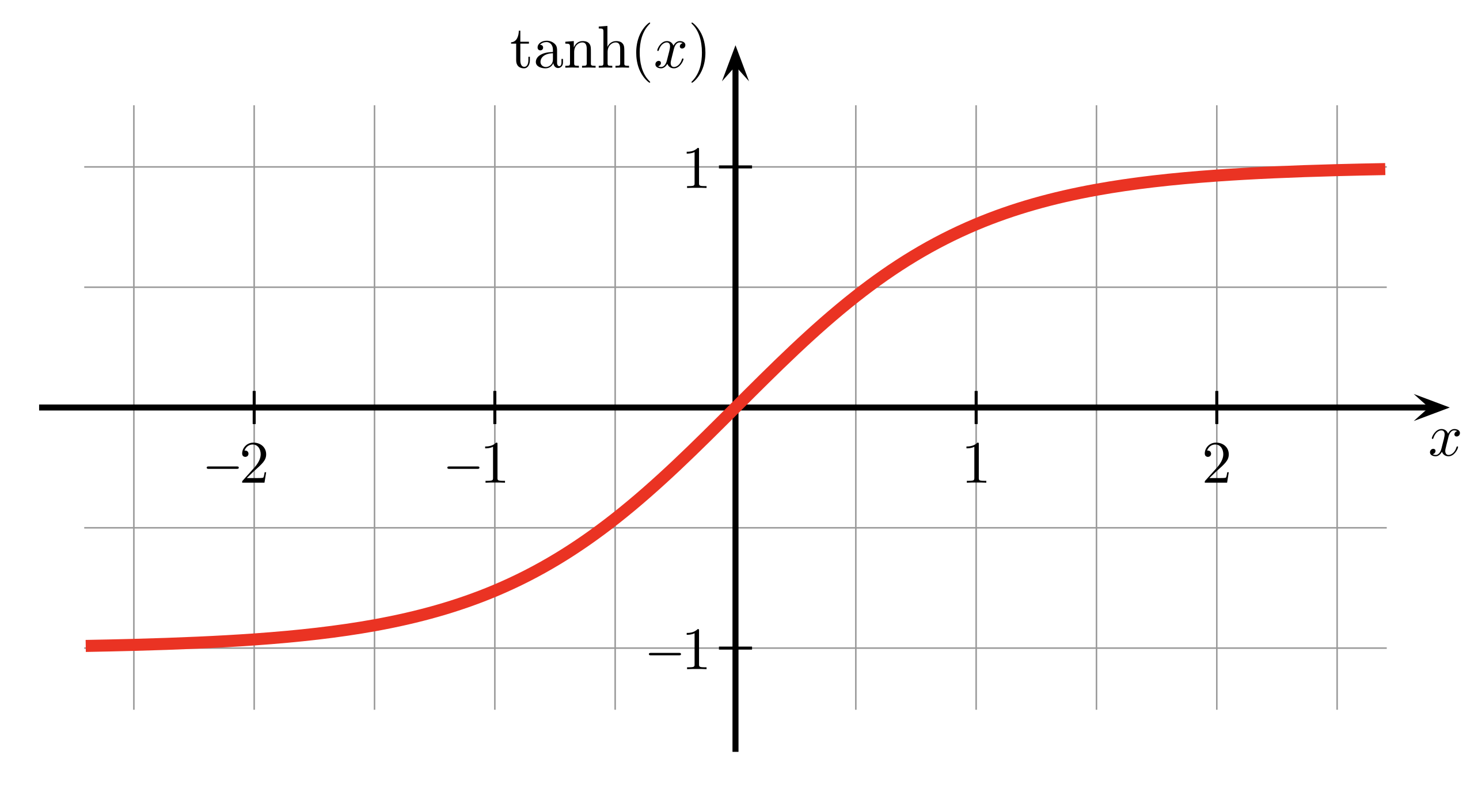
- What is tanh activation function? What is it used for?
- The range of a hyperbolic tangent function is between -1 and 1. The shape of the graph resembles that of sigmoid function. Compared to the sigmoid function, the slope increases more rapidly as $x$ approaches closer to 0. Tanh activation function can be used to represent the normalized value of a pixel(0~255).
'강의 & 책 > PyTorchZeroToAll' 카테고리의 다른 글
| [PyTorchZeroToAll] VGG-Net (Visual Geometry Group) (0) | 2022.03.18 |
|---|

