| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | |||
| 5 | 6 | 7 | 8 | 9 | 10 | 11 |
| 12 | 13 | 14 | 15 | 16 | 17 | 18 |
| 19 | 20 | 21 | 22 | 23 | 24 | 25 |
| 26 | 27 | 28 | 29 | 30 | 31 |
- CS224N
- nerf
- rl
- Perception 강의
- 컴퓨터비전
- GaN
- cv
- cl
- GAN #StyleCLIP #YAI 11기 #연세대학교 인공지능학회
- YAI
- YAI 10기
- VIT
- Fast RCNN
- YAI 11기
- 3D
- CS231n
- CNN
- NLP #자연어 처리 #CS224N #연세대학교 인공지능학회
- YAI 9기
- 자연어처리
- 강화학습
- Googlenet
- YAI 8기
- 컴퓨터 비전
- transformer
- Faster RCNN
- RCNN
- 연세대학교 인공지능학회
- NLP
- PytorchZeroToAll
- Today
- Total
연세대 인공지능학회 YAI
[논문 리뷰] NeRF : Representing scenes as Neural Radiance Fields for view synthesis 본문
[논문 리뷰] NeRF : Representing scenes as Neural Radiance Fields for view synthesis
_YAI_ 2023. 3. 4. 14:29YAI 9기 박준영님이 나의야이아카데미아팀에서 작성한 글입니다.
NeRF
: Representing Scene as Neural Radiance Fields for View Synthesis
[Mildenhall, Ben, et al. "Nerf: Representing scenes as neural radiance fields for view synthesis." Communications of the ACM 65.1 (2021): 99-106.](https://dl.acm.org/doi/abs/10.1145/3503250)
Abstract
이 논문은 input으로 한정된 수의 3D scene을 획득, 이를 활용하여 continous volumetric scene function에 입각한 여러 방향에서의 scene 정보를 얻는 것에 SOTA가 되었다. 알고리즘은 convolution을 사용하지 않고 FC layer를 사용했으며, input은 spatial location(공간 좌표)인 x, y, z와 해당 위치에서의 scene을 관찰하는 방향 파라미터인 $\theta, \phi$ 를 사용하게 된다(5차원 좌표).
이러한 5차원 좌표를 사용, camera ray를 따라 특정 값(RGB, density)들을 예측하고, 이를 volume rendering 방법을 사용하여 color와 density를 다시 image로 합성해낸다. Volume rendering의 경우 미분 가능한 공식이므로, 이렇게 생성된 synthesized scene과 실제 GT와의 비교를 통해 최적화가 가능하다.

위와 같은 그림을 참고해보자.
Introduction
View synthesis와 관련된 문제 해결 방법은 NeRF 이전에도 많이 존재했다. 나머지 방법은 간단한 task 설명 후에 related works에서 보다 자세히 풀어보도록 하자. 우선 이 논문에서 View synthesis를 해결하고자 한 방향은 optimizing parameters, 즉 딥러닝 base라는 것이다. 따라서 저자들은 우선 static scene을 연속된 5차원 함수로 표현하고자 하였다. 여기서 말하는 차원은 특정 scene을 대표할 수 있는 인자로, 해당 논문에서는 앞서 설명했듯이 공간 상에서의 위치 $(x, y, z)$ 와 관찰 방향 $(\theta, \phi)$ 을 함께 사용한 좌표계를 정의하였다. FC layer, MLP로 최적화하는 방향성은 바로 이 5차원의 input을 토대로 volume density(의미는 밀도이지만, 실질적으로는 해당 위치에 volume이 존재할 확률로 해석된다)과 RGB를 예측한다. RGB의 경우 뒤에서도 설명하겠지만 관찰 위치에 따라서 달라지는 값이 되기 때문에 view-dependent RGB color로 생각하면 된다.
NeRF는 일종의 Few-Shot learning과 같이 생각하면 되는데(물론 실제로 필요한 샘플 수는 few가 아니긴 하지만), 이는 하나의 scene에 대한 continous representation을 학습하기 위해서는 공간 전반에 걸쳐 카메라를 정렬(혹은 위치)시키고, 이러한 세팅 속에서 생성한 데이터가 최적화에 필요하기 때문이다. 이렇게 사용된 샘플, 그리고 그에 상응하는 5차원 벡터는 앞서 설명한 딥러닝 네트워크를 최적화한다. 우선 모델이 특정 위치에서의 camera ray를 따라 output query를 생성하면 이를 종합하여 scene 정보를 합성하는 형태로 함수를 구성하고, 실제 GT 와의 비교 및 미분 최적화를 통해 파라미터 세팅을 진행한다.

이 논문이 가장 큰 contribution을 가지는 점은 간단한 네트워크를 사용했다는 점이 아닐까 싶다. 또한 최적화 과정에서 3D represesntation에 대한 GT를 전혀 사용하지 않았다는 점 또한 놀랍다. 단순히 3D scene을 촬영한 2D projected image만을 사용, 최적화하여 연속적인 공간 상의 물체를 표현하려 했다. 5차원 벡터를 input으로 사용함에 있어 생성 이미지의 fidelity를 높이는 방법으로 positional embedding을 사용하였다.
Related works
실제로 3D scene을 표현하려는 방법으로 MLP 최적화를 사용한 방법은 NeRF가 유일하지는 않다. 이전에는 특정 위치($x, y, z$)에서의 거리(distance)를 통해 간단한 3D 형태를 학습 또는 최적화하는 연구도 있었다. 그러나 이러한 방법들은 3D representation(voxel grid 및 mesh)를 활용해 최적화하던 방법에 비해 얻을 수 있는 scene의 퀄리티가 상당히 저하되는 문제점이 있었다. 이 논문에서 소개한 related works를 살펴보면 크게 두 갈래로 나뉘는 것을 알 수 있는데, 이를 하나씩 살펴보도록 하자.
Neural 3D shape representations
NeRF와 비슷한 시기에 연구되었던 내용 중 하나는 앞서 언급했던 $xyz$ 좌표에 따라 signed distance(물체가 존재하는 표면과의 거리) 혹은 occupancy fields(물체가 차지하는 평면)을 예측하는 형태로 진행되었다. 그러나 이러한 연구들은 전체적인 윤곽만 잡을 뿐 실제 형태에 대해서 디테일하게 예측하지는 못한다는 단점이 존재하며, 추가적으로 3D representation이 필요하다는 문제가 있다. 3D occupancy field를 딥러닝으로 최적화하는 경우는, 3D occupancy field의 표현과 각 ray 와의 교차점을 찾는 것이고 이렇게 예측된 각 포인트마다 color를 예측하게 된다. 만약 이(3D occupancy field)를 직접적으로 사용하지 않는다면 단순히 feature vector와 각 좌표에서의 연속적인 RGB color를 내보내고, RNN을 통해 ray의 각 지점마다 surface 존재 여부를 판별하게 된다.
물론 위와 같은 연구들이나 기술들 또한 복잡하거나 고화질의 형태를 예측할 수 있지만, 간단한 형태에 대해서만 최적화가 된다던가 rendering 시에 표면이 제대로 표현되지 않고 oversmooth되어 보인다. 이는 loss를 최적화하는 과정에 있어 distance 및 occupancy field와의 loss를 최적화할 때, overfitting을 방지하기 위한 방향성 때문이라고 생각된다.
따라서 NeRF에서는 3차원 공간 좌표가 아닌 이에 추가적으로 방향성에 대한 정보를 더한 5차원 벡터 $(x, y, z, \theta, \phi)$ 를 사용하여, 특정 방향에서 바라본 보다 photorealistic하고 고화질의 2D representation을 획득할 수 있게끔 하였다.
View synthesis and image-based rendering
만약 시점에 대한 샘플링이 많이 진행된다면(보다 연속적인 view에 대한 샘플링이 이루어진다면), 단순히 특정 시점에서의 photorealistic view는 light field의 보간을 통해 획득할 수 있다(구체적인 방법은 복잡하기 때문에 생략하지만, Camera geometry와 관련된 내용이라고 간단하게 짚고 넘어가도록 하겠다). 그렇지 않고 만약 보다 적은 샘플링이 진행되었을 경우, computer vision 및 graphic 연구에서는 관찰된 이미지들을 통해 geometry를 예측하게 되고, 이는 충분히 많은 성과를 이뤄가고 있었다.
예측할 수 있는 representation 중 가장 유명한 방법은 mesh-based로, diffusion 방식(generative model에서 해석하는 diffusion의 뜻과 동일)으로 표면을 색칠하거나, view 방향에 따라 어떻게 보이는지 결정하는 형태의 연구로 구분될 수 있다.
컴퓨터 그래픽스(graphics)에서 Clipping(clip space로 옮긴 다음 공간 밖의 물체를 자르는 작업), Perspective division(원근법을 구현), Back-face culling(실제 사물을 보는 시각에서 메쉬의 각도에 따라서 시각적인 처리해주는 것), Surface normal(메쉬를 구성하는 vertex의 순서에 따라 앞면과 뒷면을 구분하는 것) 그리고 viewpoint transform(clip space에서 시각적인 공간으로 옮기는 것)과 마지막으로 Scan conversion(메쉬 삼각형 내부의 fragment를 생성하는 것 - 보통 interpolation으로 이해하면 된다)를 진행하는 Rasterizer가 있는데, 메쉬를 시각화하는 프로세스 자체를 미분 가능한 형태로 만들기도 하며, 언리얼 엔진에서 많이 사용되는 Path tracing 또한 미분 가능한 형태로 만들어 최적화하기도 한다([https://en.wikipedia.org/wiki/Path_tracing](https://en.wikipedia.org/wiki/Path_tracing)). 미분 가능한 형태로 image reprojection을 진행(tracer의 역과정으로 backpropagation)하는데, 이때 local minima에 빠질 확률이 높고 loss landscape가 복잡한 형태에 대해 최적화하기 힘들다는 단점이 있다. 또한 mesh 형태로 scene이 구성되어야 한다는 제약 때문에, 배경이나 물체의 형태가 다양하게 등장하는 real-world scene에 대해서는 synthesizing하기 힘들다는 문제도 존재한다.
앞선 방법과 다른 형태의 방법으로는 volumetric representation을 사용하여 최적화하는 방식이 있는데, mesh based에 비해 artifact가 현저히 줄어들 수 있는 형태가 되며 보다 사실적인 디테일을 살릴 수 있는 방법이다. 초기 연구들은 관찰된 이미지와 color voxel grid를 직접적으로 접근시키는 방법을 사용했으며, 보다 최근에는 여러 방향에서의 scene을 딥러닝을 통해 최적화, 이를 토대로 수집된 이미지에 대한 입체 representation를 생성하는 연구도 진행되었다. 다중 시각에 대해서 최적화한 representation을 alpha summation을 하거나 학습된 summation을 통해 새로운 view를 생성하게 된다. 다른 형태의 연구로는 CNN과 특정 scene에서의 voxel grid를 융합하여 최적화하는 방식이 있다.
이렇게 부피(공간)를 대표하는 형태를 기반으로 최적화하는 기술들은 좋은 결과를 보여주었지만, 보다 고화질의 이미지로 확장하는 면에 있어서 sampling과 시간 사이의 trade off가 심하다는 문제가 있다.
Scene Representation
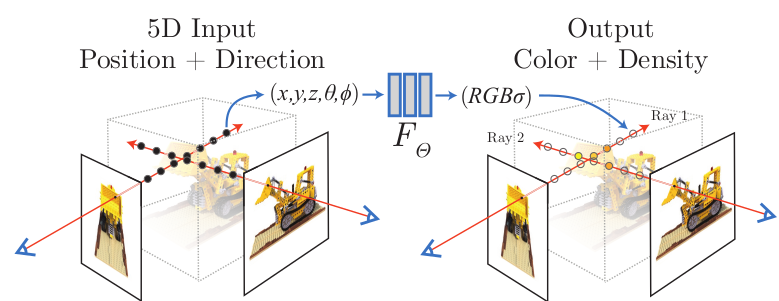
앞서 사용된 그림 중 일부를 발췌하였다.
이 논문에서 5차원 벡터를 기반으로 연속적인 이미지를 구상하는데 있어서, 각 위치에 대해 RGB 값과 density를 함수의 output으로 가지게 된다. 물론 딥러닝(MLP)를 사용하기 때문에, deterministic한 함수가 아닌 parameterized function인 $F_{\Theta}$ 를 최적화하게 된다. 논문에서는 위치 벡터에 해당되는 3차원 좌표 $(x, y, z)$ 를 $\rm{x}$, 방향에 대한 정보인 2차원 벡터 $(\theta, \phi)$ 를 $\rm{d}$ 라고 명시한다. 이렇게 공간 전반에 걸쳐 representation이 학습되면, 이 학습된 전체 정보는 네트워크 내부에서 처리되는 것이다. 또한 네트워크 학습에 있어 constraints를 주기 위해 RGB color인 $\rm{c}$ 는 위치 및 방향에 대해서 모두 예측되게끔 하고, 밀도인 $\sigma$ 는 위치에 대해서만 예측되게 하였다. 이는 물체의 scene을 합성하는데 있어서 RGB는 방향에 따라 달라질 수 있지만, 같은 위치에서의 density는 같아야 하기 때문이다.
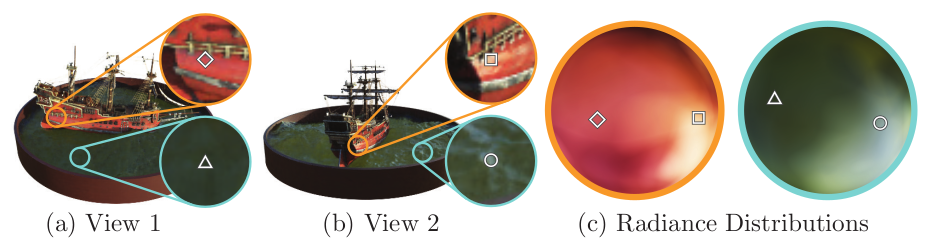
이를 단적으로 보여주는 예시가 바로 위와 같은데, View 1에서의 다이아몬드와 View 2에서의 사각형 위치의 색이 서로 다른 것을 확인할 수 있다. 실제로 학습된 네트워크를 기반으로 전체 방향에서의 interpolation을 (c)에서 Radiance Distribution으로 그렸는데, 색 변화가 viewing direction에 대해 연속적으로 변해가는 것을 확인할 수 있다.
Volume rendering
위와 같이 네트워크가 학습되면 위치에 따라서 연속적인 공간에 대한 정보를 학습하게 된다. 그렇다면 이렇게 학습된 값들을 기반으로 scene을 구상하는 법을 생각해보도록 하자.
5차원 neural radiance field는 volume density와 특정 포인트에서의 색으로 표현된다고 하였다. 즉, 어떠한 ray가 있다면, 그 ray의 모든 점에 대해서 volume density $\sigma(\rm{x})$ 는 location $\rm{x}$ 까지(그 위치에서 끝나는) 향하는 ray 상에서의 확률 차이(정확히 말하자면 이를 연속적인 미소 dt에 대해서 분배)라고 볼 수 있다. 이게 무슨 말이냐면, 관찰을 시작하는 부분을 기준으로 특정 지점($\rm{x}$) 까지의 확률 누적이라고 볼 수 있다는 것. 이를 식으로 표현하자면 $\rm{r}(t) = \rm{o}+t\rm{d}$ 로 표현되는 ray 직선의 방정식에 대해 가까운 bound $t_n$ 부터 가장 먼 bound인 $t_f$ 까지에서의 color expectation을 구할 수 있다는 것이다.
$$C(\rm{r}) = \int^{\it{t_f}}_{\it{t_n}} \it{T(t)} \sigma(\rm{r}(\it{t})) \rm{c}(\rm{r}(\it{t}), \rm{d})\it{dt}
$$
$$T(t) = \exp \left( -\int_{t_n}^t \sigma(\rm{r}(\it{s})) \it{ds}\right)
$$
바로 위에서 설명했듯, scene에서의 색은 바라보는 방향과 위치 모두의 함수이므로 이 둘을 모두 인자로 가지게 되고 scene에서의 밀도는 위치에 대한 인자만 input으로 가지게 된다. $T(t)$ 는 직선 상의 지점 $t$ 까지의 밀도에 대한 확률 누적으로, 지점 $t_n$ 까지 진행하는 ray가 물체와 충돌하지 않을 확률(사이에 아무런 object가 존재하지 않을 확률)로 해석 가능하다. 다르게 표현하자면 $C(\rm{r})$은 해당 위치, 방향에서의 RGB 값이 특정 density로 존재할 확률에 대한 expectation을 구한 식과 같다. 흔히 discretized 형태의 grid를 렌더링할 때 구분구적법을 사용하게 되는데(연속된 샘플을 얻을 수는 없으므로), 이 경우 특정 location에 대한 정보만 MLP가 query되므로 representation의 resolution이 앞서 언급한 기존 방식과 크게 다르지 않게 제한되는 문제가 발생한다. 따라서 대신에 해당 논문에서는 stratified sampling을 사용하였고, 이는 ray가 퍼져가는 특정 구획을 N으로 균일하게(각 bin 사이 간격이 일정) 샘플링한 상태에서 각 bin 사이에서 하나의 sample를 uniform하게 가져오는 형태를 취하였다. 즉,
$$t_i \sim U \left[ t_n+\frac{i-1}{N}(t_f-t_n),\sim t_n + \frac{i}{N}(t_f-t_n) \right]
$$
위와 같은 식처럼, $1/N$로 분할된 영역 내에서 랜덤으로 위치를 뽑는데, 그 랜덤 방식이 uniform distribution을 따른다고 생각하면 된다. 이를 통해 모델이 학습하는데 있어서 보다 다양한 position sample에 대해 최적화가 가능해진다. 비록 계산을 위해 불연속 점들에 대한 cumulation이 적분을 대체하지만, 이를 샘플링으로 어느 정도 커버한 것을 확인할 수 있다. 즉, 실제로 모델이 학습하고, 이를 토대로 렌더링하는 $C(\rm{r})$의 근사치인 $\hat{C}(\rm{r})$은,
$$\hat{C}(\rm{r}) = \sum_{i=1}^N T_i(1-\exp(-\sigma_i \delta_i))\rm{c}_i
$$
이고, 여기서 $T_i$는,
$$T_i = \exp \left( -\sum_{j=1}^{i-1} \sigma_j \delta_j\right)
$$
위와 같이 summation으로 전환 가능하다. $\delta$로 표현된 것은 인접한 두 샘플 사이의 간격으로, 기존의 $dt$를 대체한다고 보면 된다.
Optimizing a Neural Radian Field
전체적인 개요, 선행연구 그리고 어떤 식으로 Neural network를 최적화할지에 대해 개념적인 리서치는 모두 언급하였다. 그러나, 단순히 이런 이론만 가지로 연구를 진행했을 경우 SOTA 퀄리티가 나오지 않는 것을 확인하였고, 저자들은 이를 해결하기 위해 두 가지 추가 방법론을 제시한다. 그 중 첫 번째는 positional encoding을 추가하여 좌표에 추가 차원(dimension) 효과를 준 것이고, 두 번째는 hierarchical sampling이다.
Positional encoding
Neural network 자체는 함수 형태를 최적화하기 위해 좋은 형태로 작용하지만, 단순히 $F_\Theta$를 $xyz\theta \phi$에 최적화하는 작업은 생각보다 high-quality 정보를 읽어버리는 결과를 낳았다. 이는 deep neural network과 lower frequency function에 치우치게 된다는 문제 때문인데, 일반적으로 딥러닝 모델은 최적화 방향을 향해 찾아가기 때문에 이러한 문제가 발생할 수 있다. 또한 앞선 다른 연구들에 따르면, input에 higher dimensional space를 더해줄 수 있는 함수를 이용하여 모델을 최적화하면 이러한 경향성을 줄일 수 있다는 것이다. 따라서 network를 두 부분으로 분리, 이를 합성하는 형태로 바꾸게 되었는데 $R$로부터 고차원 임베딩 공간 $R^{2L}$로 보낼 수 있는 deterministic encoder를 사용(학습 불가능)한 후, 이를 기반으로 $F’_{\Theta}$를 최적화하게 된다.
Positional encoding은 가장 잘 알려져있는 sinusoidal encoding인,
$$\gamma(p) = ( \sin(2^0\pi p), \cos(2^0 \pi p), \cdots, \sin(2^{L-1}\pi p), \cos(2^{L-1} \pi p) )
$$
을 사용한다. 인코딩 함수인 $\gamma$는 x, y, z 세 좌표 모두에 각각 적용된다. 이때 좌표는 $[-1, 1]$로 정규화된 상태다. 마찬가지로 인코딩 함수는 방향 벡터인 $\rm{d}$에도 적용된다. 이 논문에서 실험 세팅은 $\rm{x}$(위치 벡터)에 대해서는 $L=10$을 적용하였고, $\rm{d}$(방향 벡터)에 대해서는 $L = 4$를 적용하였다.
이러한 포지션 임베딩을 적용하는 대표적인 예시로는 transformer architecture가 있다. Transformer는 이를 inductive bias를 더해주는(각 토큰 위치 정보를 통해) 형태로 작용하게 되었으나, 이 논문에서는 좌표를 보다 고차원의 정보로 임베딩하기 위해 사용했다는 점이 차이가 될 수 있겠다.
Hierarchical volume sampling
계층적 샘플링은 고전적으로 많이 사용되는 샘플링 방법 중 하나다. 결론부터 말하자면 이를 활용하는 이유는 실제 ray 상에서 물체가 존재하는(density가 있는) point는 극히 일부에 해당되며, 이는 마치 이미지에서 foreground보다 background 영역이 큰 것과 비슷한 상황이다. Object detection 네트워크에서도 학습할 때 foreground, background 샘플의 분포가 많이 차이나는 것 때문에 bias가 생기는 것을 우려하여 계층적 샘플링을 통해 분포를 맞춰주는 작업을 하는 것을 확인할 수 있다.
따라서 단순히 하나의 네트워크를 최적화하기 보다, 두 네트워크를 동시에 최적화하는 방법을 사용하였다. 이를 각각 ‘Coarse(거친, 날것의)’ 네트워크와 “fine(정교한, 세심한)” 네트워크로 명명한다. 먼저 위에서 언급했던 것과 같이 $N_c$ 개의 location을 stratified sampling을 통해 랜덤으로 뽑아내고, $\hat{ C}(\rm{r})$를 예측하는 형태로 coarse network를 evaluate하게 된다. 이렇게 추출된 output을 기반으로, volume에 보다 관련이 있는 영역으로 샘플을 맞춰주게 된다. 이를 위해 가장 먼저
$$\hat{C}_c(\rm{r}) = \sum_{i=1}^N \it{w}_i\rm{c}_i,~\it{w}_i = T_i(1-\exp(-\sigma_i \delta_i))\rm{c}_i
$$
위와 같이 추출된 color를 ray를 따라서 오는 모든 sample color $c_i$의 weighted sum으로 표현하고, 이러한 weight 전체를 normalize하여 확률값으로 바꿔준다.
$$\hat{w}_i = \frac{w_i}{\sum_{j=1}^{N_c} w_j}
$$
각 위치에 대한 확률값으로 바뀐 이 value를 통해 다시 샘플링하게 된다. weight가 큰 값을 가지는 곳이 곧 coarse network가 evaluate했을 때 물체가 있을 확률(밀도)가 큰 영역이므로, 이 부분 위주로 샘플링하는 것이다. 이렇게 추가로 추출된 $N_f$ 샘플을 추가로 사용하여 fine network를 evaluate하면, 결론적으로 최종 rendered color인 $\hat{C}_f(\rm{r})$을 획득하게 된다. 이는 비균일한 확률 분포를 가지는 샘플링과 비슷하지만, 샘플된 value 자체를 전체 적분 영역에서 non uniform 이산화(quantization)하기 위한 확률 값으로 사용하였다.
Optimization
최적화하기 위해서 요구되는 것은 RGB image scene과 각 scene에 대한 camera pose, intrinsic, bound 등 여러 corresponding 정보들이다. 최적화 단계에서는 camera rays의 배치에서 랜덤하게 추출하고, coarse network와 fine network를 기반으로 계층적 샘플링을 진행한다. Loss는 정말 간단하게도 추정된 color(렌더링 과정을 거쳐서 생성된 pixel 값)과 실제 값을 비교하는 squared error loss를 사용한다.
$$L = \sum_{r \in R} \left[ \parallel \hat{C}_c(\rm{r}) - \it{C}(\rm{r}) \parallel_2^2 + \parallel \hat{\it{C}}_{\it{f}}(\rm{r}) - \it{C}(\rm{r}) \parallel_2^2 \right]
$$
각 notation이 의미하는 바는 다음과 같다.
- $\it{C}(\rm{r})$ : Grount truth color
- $\it{\hat{C}}_c(\rm{r})$ : coarse volume color prediction
- $\it{\hat{C}}_f(\rm{r})$ : fine volume color prediction
- $R$ : rays pool(batch 내부의 모든 ray를 의미)
Experiment setting detail
실험에서는 4096 batch size의 ray를 사용, 이는 coarse 하게 추출된 $N_c = 64$와 이를 토대로 추출된 $N_f = 128$을 기반으로 한다. Optimizer는 Adam을 사용하였으며, $5 \times 10^{-4}$ 부터 $5 \times 10^{-5}$ 까지 exponentially 줄어들게끔 learning rate을 사용하였다. 하나의 scene을 최적화하는데 약 100
300k iteration이 들며, 이는 저자들이 실험한 세팅에서 약 1
2일 걸렸다고 한다(오래 걸리는게 이 모델의 단점인 것 같다).

Results
실제로 위의 표를 보면, 성능 지표로 사용된 PSNR, SSIM 그리고 LPIPS 등 여러 부문에서 NeRF가 좋은 성능을 보이는 것을 볼 수 있다. [NeRF project page](https://www.matthewtancik.com/nerf)에 들어가보면 보다 자세한 결과를 확인해볼 수 있다.
Dataset
Synthetic renderings of objects
이 논문에서 결과를 보이기 위해 사용한 데이터는 크게 두 가지다. 첫 번째는 DeepVoxels dataset으로, 이는 총 4개의 Lambertian(어느 방향에서 보아도 조광이 일정하다(균일하다)는 뜻) 물체가 간단한 geometry로 구상된 형태의 데이터셋이다. 각 object는 $512 \times 512$ 픽셀로 viewpoint에서 렌더링되며(반구의 위쪽에서 관찰된 이미지 형태), 479 샘플은 input으로, 1000 샘플은 test에 사용되었다. 또한 추가적으로 보다 사실적인 scene에 대한 데이터셋인 복잡한 기하학적 형태를 가진 non-Lambertian(방향에 따라 물체의 겉면 색이 달라진다는 뜻)물체 8개와, 각각의 pathtraced image를 포함한 형태의 데이터셋을 구성하였다. 여섯은 반구 위쪽에서 관찰된 이미지 형태를 렌더링하고, 둘은 구 전체(물체의 아래 부분까지 포함)에 대한 viewpoint를 렌더링하였다. 모두 $800 \times 800$ 의 픽셀 사이즈를 가지며, 100개의 view를 input으로 사용하고 200개를 test에 사용하였다. 위의 표에서 Diffuse Synthetic이 의미하는 것이 곧 Lambertian, Realistic Synthetic이 의미하는 것이 non-Lambertian이라고 보면 된다.
Real images of complex scenes
또한 이 논문에서는 복잡한 형태의 현실 scene을 앞쪽에서 본 모습을 사용하였는데, 총 8개의 scene을 사용하였다. 이 중 5개는 LLFF paper에서 온 장면이고, 3개는 저자들이 직접 캡처했다고 한다. 20~62개의 이미지가 캡처되었고, 이중 1/8은 test에 사용하였다. 모든 렌더링 이미지의 크기는 $1008 \times 756$ 픽셀 사이즈를 가진다.
Model comparisons
NeRF 모델의 성능을 확인해보기 위해, 다른 view synthesis 기술 중 좋은 성능을 보이는 모델들과 비교하였고, 이를 실제로 시각적으로 페이퍼에 기재하였다. 모든 기술들은 같은 input view에 대해 학습하고(Local Light Field Fusion은 제외) 그 성능을 비교하였다.
Neural Volumes(NV)
[Neural Volumes](https://research.facebook.com/publications/neural-volumes-learning-dynamic-renderable-volumes-from-images/)는 분리된 배경(무조건 object를 제외하고 촬영이 되어야 함) 정면에 존재하는 bounded volume의 view를 합성한다. 최적화는 deep 3D convolutional network를 사용하고, 불연속적인 RGB$\alpha$ 값을 voxel grid마다 ($128^3$ 샘플 사용) 예측하고 동시에 3D warp grid를 $32^3$ 샘플로 예측하게 된다. 전체적인 알고리즘은 아래 그림에서 볼 수 있듯이, marching camera ray를 warped voxel grid에 렌더링하는 방식으로 진행된다.
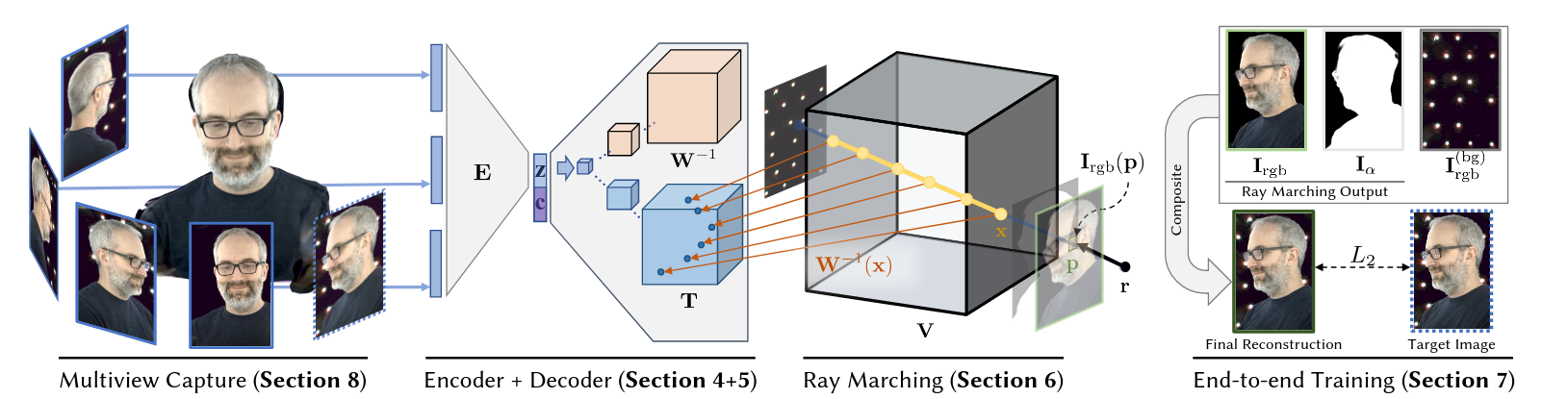
Scene Representation Networks(SRN)
SRN은 연속적인 장면을 불투명한 형태의 표면(surface)로 표현하고자, MLP를 활용하여 각 $(x, y, z)$ 좌표에 대한 feature vector를 추출한다. 그리고 RNN 구조를 활용하여 ray를 따라 진행하게 되고, 이때 앞서 추출된 feature vector를 사용한다. 각 state에서 내보내는 output은 곧 matching step size를 결정하게 된다(ray를 따라서 이동하는 형태로 생각). 최종단에서 추출되는(decoding 되는) feature vector는 output으로써 마지막 위치에서의 surface color를 디코딩한다.
Local Light Field Fusion
LLFF는 forward facing scene(앞에서 본 이미지)를 기반으로 사실적인 novel view를 만들기 위해 디자인된 모델이다. 학습된 3D convolutional network를 사용하여 RGB$\alpha$ 그리드를 생성하고, alpha compositing과 nearby MPI를 활용하여 novel scene을 렌더링하는 방식이다.
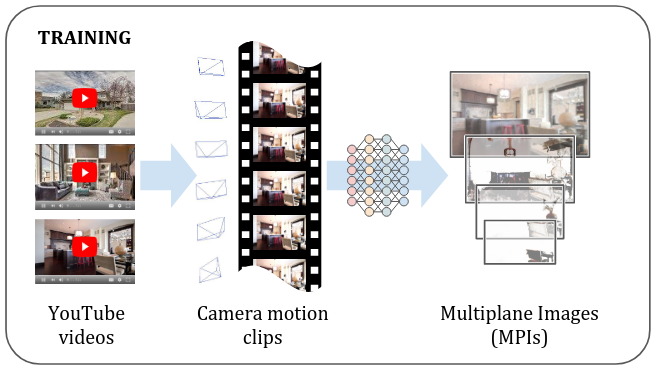
MPI 예시 그림. marching된 씬을 따라 움직이면 multiplane image를 생성할 수 있다는 형태로 이해하면 쉽다
Comparison results


결과도 잘 나오는 것을 확인 가능.
Discussion
잘 나왔다는 점이 눈에 가장 먼저 보인다. 디테일한 부분들을 살리지 못했던 기존 방식에 비해 NeRF는 3D representation 정보를 사용하지 않고도 충분히 detail을 살린 결과들을 보여주었다. 그러나 실용적으로 사용되기 힘들었던 점은 시간과 공간 표현 대비 trade-off가 너무 큰 문제로 작용했기 때문인데, 예를 들어 기존 방식의 LLFF와 같은 경우 시간은 다소 적게 걸리지만 그만큼 Realistic Synthetic scene을 위한 메모리 차지가 심하다는 단점이 있었다. 그에 비해 NeRF는 네트워크 자체는 상당히 간단한 편에 속하기 때문에, 다양한 데이터셋에 대해서도 최적화가 가능하다는 장점이 있다.
FC layer structure
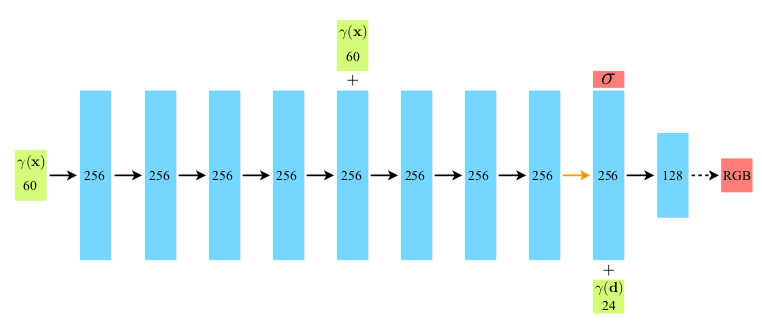
위는 fully-connected network 구조, positional encoding이 더해진 형태의 위치 정보$(\gamma(\rm{x}))$ 를 input으로 넣어주게 되고, 256 채널과 ReLU로 엮인 총 8개의 네트워크를 통과하게 된다. 해당 논문에서는 DeepSDF 구조를 따르고, skip connection을 5번째 layer의 activation에 넣어주게 된다.
또한 추가 레이어는 volume density인 $\sigma$ 를 output으로 내보내게 되는데, 이때 output은 non-negative임이 보장되어야 하므로 ReLU를 사용하여 rectify한 output을 사용하였다. density와 함께 추출된 256의 채널로 구성된 feature 정보는 이후 방향 벡터가 인코딩된 정보$(\gamma(\rm{d}))$ 와 함께 마지막 레이어를 통과하면서 RGB 값을 추출해낸다.
NDC ray space derivation
forward facing scene을 만들기 위해서 NDC space라는 개념이 사용된다. 행렬이 무자비하게 나오는 파트라서 간단하게만 짚어보고 넘어가는게 좋을 것 같다.
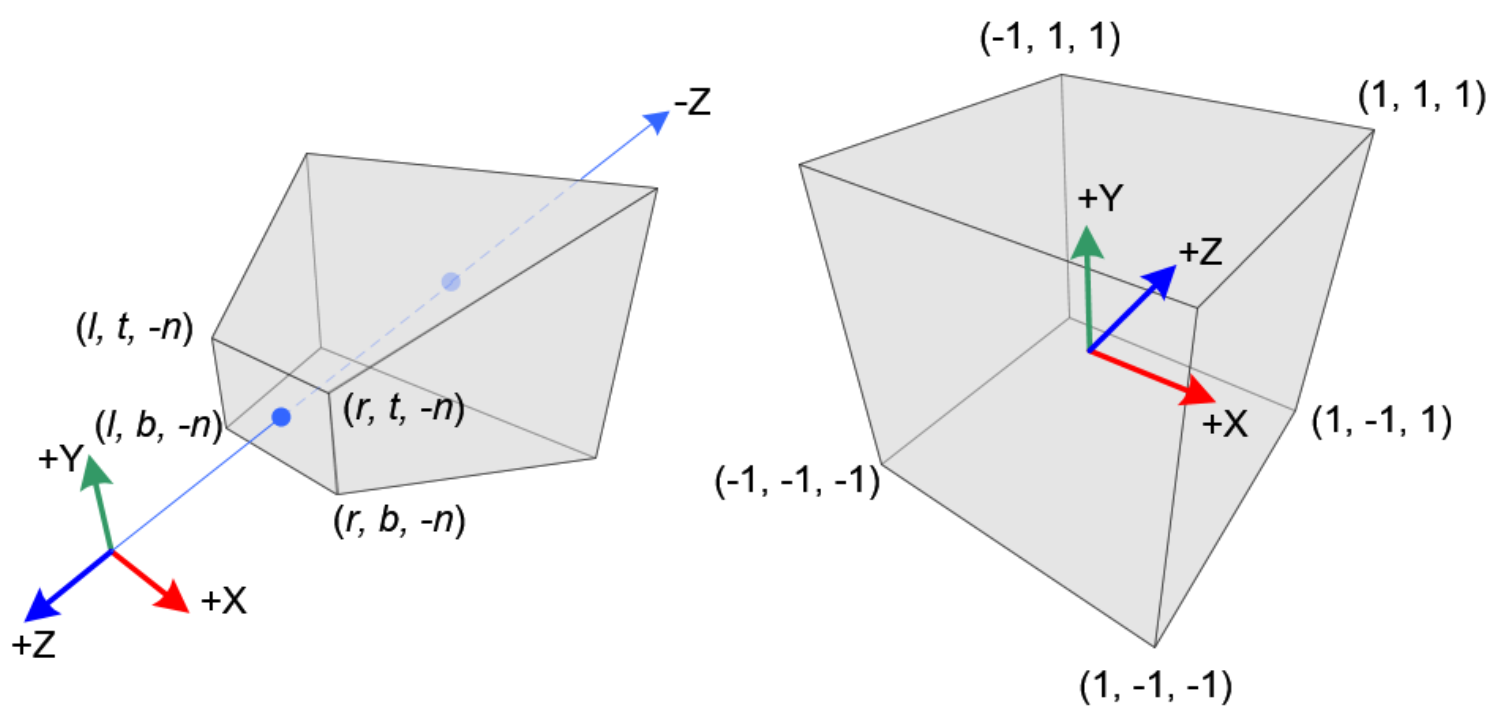
NDC는 쉽게 말해서 카메라가 인지하는 공간적인 형태를 고르게 펴서 cube 형태로 맞춰주는 작업을 의미한다. 우리가 흔히 알고 있는 기본적인 3D perspective projection matrix는 homogeneous 좌표계에 따라서,
$$M = \left(
\begin{array}{cccc}
\frac{n}{r} & 0 & 0 & 0 \\
0 & \frac{n}{t} & 0 & 0 \\
0 & 0 & \frac{-(f+n)}{f-n} & \frac{-2fn}{f-n} \\
0 & 0 & -1 & 0
\end{array}
\right)
$$
위와 같이 표현 가능하다. $n, f$ 는 가각 clipping plane 까지의 거리라고 보면 되고, $r, t$ 는 각각 오른쪽과 위쪽 bound(가까운 clipping plane)를 의미한다. 위의 그림에 얼추 나와있으니 보면서 이해하면 좋다.
Homogeneous point인 $(x, y, z, 1)^T$ 를 프로젝션하기 위해, M을 곱하고 마지막 coordinate으로 정규화를 진행한다. 자세한 내용은 Homogeneous 관련 lecture를 들으면 된다.
$$M = \left(
\begin{array}{cccc}
\frac{n}{r} & 0 & 0 & 0 \\
0 & \frac{n}{t} & 0 & 0 \\
0 & 0 & \frac{-(f+n)}{f-n} & \frac{-2fn}{f-n} \\
0 & 0 & -1 & 0
\end{array} \right)
\left( \begin{array}{c}
x \\
y \\
z \\
1 \\
\end{array}\right) =
\left( \begin{array}{c} \frac{n}{r}x \\ \frac{n}{t}y \\ \frac{-(f+n)}{f-n}z-\frac{-2fn}{f-n} \\ -z \end{array} \right)
$$
여기서, 프로젝션된 좌표를 다시 원래의 좌표로 바꾸게 되면
$$\text{Project} \rightarrow
\left( \begin{array}{c} \frac{n}{r}\frac{x}{-z} \\ \frac{n}{t} \frac{y}{-z} \\ \frac{(f+n)}{f-n}-\frac{2fn}{f-n} \frac{1}{-z} \end{array} \right)
$$
이제 NDC space에 놓여있게 되므로, 우리는 특정 ray 벡터 $\rm{o}+\it{t}\rm{d}$ 상의 모든 point를 NDC space인 $\rm{o^\prime}+\it{t^\prime}\rm{d^\prime}$ 옮기는 것이 목표다. 앞서 구한 projection point들을 다음과 같이 바꿔쓰도록 하자.
$$\text{Project} \rightarrow
\left( \begin{array}{c} \frac{n}{r}\frac{x}{-z} \\ \frac{n}{t} \frac{y}{-z} \\ \frac{(f+n)}{f-n}-\frac{2fn}{f-n} \frac{1}{-\end{array} \right) =
\left( \begin{array}{c} a_xx/z\\ a_yy/z \\ a_z+b_z/z \end{array} \right)
$$
그렇게 되면 projection 되는 $o^\prime$ 그리고 direction $d^\prime$ 은 다음을 만족해야한다.
$$\left( \begin{array}{c}
a_x \frac{o_x+td_x}{o_z+td_z} \\
a_y \frac{o_y+td_y}{o_z+td_z} \\
a_z+\frac{b_z}{o_z+td_z}
\end{array} \right) =
\left( \begin{array}{c}
o^{\prime}_x+t^{\prime}d^{\prime}_x \\ o^{\prime}_y+t^{\prime}d^{\prime}_y \\
o^{\prime}_z+t^{\prime}d^{\prime}_z
\end{array}
\right)
$$
그러나 위의 식은 constraint가 없어 너무 변수가 많아지므로 식이 복잡하다. 간단하게 표현하기 위해 starting point를 기준으로 식을 바꾸면,
$$\left( \begin{array}{c}
a_x \frac{o_x}{o_z} \\
a_y \frac{o_y}{o_z} \\
a_z+\frac{b_z}{o_z}
\end{array} \right) =
\left( \begin{array}{c}
o^{\prime}_x \\ o^{\prime}_y \\
o^{\prime}_z
\end{array}
\right) = o^\prime = \pi(o)
$$
위와 같고, 정확히 origin $o$ 를 projection한 대칭 point가 $o^\prime$ 임을 확인할 수 있다. 이를 다시 역으로 적용해서 변수 $t$ 가 그대로 살아있는 형태로 적용하면,
$$\begin{aligned}
\left( \begin{array}{c}
t^{\prime}d^{\prime}_x \\ t^{\prime}d^{\prime}_y \\
t^{\prime}d^{\prime}_z
\end{array}
\right) =&
\left( \begin{array}{c}
a_x \frac{o_x+td_x}{o_z+td_z}-a_x \frac{o_x}{o_z} \\
a_y \frac{o_y+td_y}{o_z+td_z}-a_y \frac{o_y}{o_z} \\
a_z+\frac{b_z}{o_z+td_z}-a_z-\frac{b_z}{o_z}
\end{array} \right) \\
=& \left( \begin{array}{c}
a_x \frac{td_z}{o_z+td_z}\left( \frac{d_x}{d_z}-\frac{o_x}{o_z}\right) \\
a_y \frac{td_z}{o_z+td_z}\left( \frac{d_y}{d_z}-\frac{o_y}{o_z}\right) \\
-b_z\frac{td_z}{o_z+td_z}\frac{1}{o_z}
\end{array} \right)
\end{aligned}
$$
위의 식에서 $t$ 에 대한 부분을 제외하고 나면 남는 $d^\prime$ 의 형태는 다음과 같다.
$$\left( \begin{array}{c}
a_x \left( \frac{d_x}{d_z}-\frac{o_x}{o_z}\right) \\
a_y \left( \frac{d_y}{d_z}-\frac{o_y}{o_z}\right) \\
-b_z\frac{1}{o_z}
\end{array} \right)
$$
다시 원래 사용했던 original projection matrix의 constants로 식을 정리하면,
$$o^{\prime} = \left( \begin{array}{c}
a_x \frac{o_x}{o_z} \\
a_y \frac{o_y}{o_z} \\
a_z+\frac{b_z}{o_z}
\end{array} \right) =
\left( \begin{array}{c}
-\frac{f_{cam}}{W/2} \frac{o_x}{o_z} \\
-\frac{f_{cam}}{H/2} \frac{o_y}{o_z} \\
1+\frac{2n}{o_z}
\end{array} \right)
$$
$$d^\prime = \left( \begin{array}{c}
-\frac{f_{cam}}{W/2} \left( \frac{d_x}{d_z}-\frac{o_x}{o_z}\right) \\
-\frac{f_{cam}}{H/2} \left( \frac{d_y}{d_z}-\frac{o_y}{o_z}\right) \\
-2n\frac{1}{o_z}
\end{array} \right)
$$
위와 같이 표현 가능하다.
'컴퓨터비전 : CV > 3D' 카테고리의 다른 글
| Instant Neural Graphics Primitives with Multiresolution Hash Encoding (1) | 2022.09.26 |
|---|---|
| [논문 리뷰] NeRF: Representing Scenes as Neural Radiance Fields for View Synthesis (0) | 2022.05.17 |


