| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | ||||
| 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 11 | 12 | 13 | 14 | 15 | 16 | 17 |
| 18 | 19 | 20 | 21 | 22 | 23 | 24 |
| 25 | 26 | 27 | 28 | 29 | 30 | 31 |
- YAI 9기
- 3D
- cl
- PytorchZeroToAll
- 연세대학교 인공지능학회
- nerf
- CNN
- 자연어처리
- YAI 10기
- GAN #StyleCLIP #YAI 11기 #연세대학교 인공지능학회
- CS224N
- Perception 강의
- Googlenet
- NLP
- cv
- 컴퓨터비전
- NLP #자연어 처리 #CS224N #연세대학교 인공지능학회
- 컴퓨터 비전
- transformer
- 강화학습
- GaN
- RCNN
- YAI 11기
- CS231n
- YAI
- rl
- YAI 8기
- VIT
- Fast RCNN
- Faster RCNN
- Today
- Total
연세대 인공지능학회 YAI
[논문 리뷰] Do Transformers Really Perform Badly for Graph Representation? 본문
[논문 리뷰] Do Transformers Really Perform Badly for Graph Representation?
_YAI_ 2023. 3. 4. 14:24Do Transformers Really Perform Badly for Graph Representation?
Github: https://github.com/Microsoft/Graphormer
Paper: https://openreview.net/forum?id=OeWooOxFwDa
Abstract
Graph representation learning에서 Transformer가 좋은 성능을 보이는가?
Graphormer
- standard transformer architecture
- 많은 graph representation learning task에서 좋은 성능을 보임
- especially on the recent OGB Large-Scale Challenge
Key Insight
- graph를 모델링하기위해 structural information을 효율적으로 encoding하는 방법의 필요성
- Graphormer의 표현력을 수학적으로 characterize
- graph의 structural information을 encoding하는 방법을 다른 GNN variants와 비교해보았을 때, 이들을 모두 Graphormer의 특수케이스로 커버할 수 있었음
1. Introduction
Graph representation에 transformer를 적용하고자 하는 꾸준한 시도
- 하지만 지금까지 가장 효과적인 방법은 feature aggregation과 같은 classic GNN variants의 몇몇 key module에만 softmax attention을 적용하는 방식
- → graph representation learning에 transformer 를 적용하는것이 적절한지에 대한 의문
Graphormer
- standard transformer architecture
- graph-level prediction task에서의 SOTA(OGB-LSC)
Transformer
- sequence modeling을 위해 고안되었음
- 이러한 특성을 그래프에 적용하기 위한 key
- 그래프의 구조적 정보를 모델에 적절히 포함시키는 것
- node $i$의 self-attention
- 노드쌍 사이의 relation으로 확인할 수 있는 structural information을 고려하지 않음
- node $i$와 다른 노드들 사이의 semantic similarity만 계산
- Graphormer는 효과적인 몇몇 structural encoding을 포함
- Centrality Encoding
- 목적 : 그래프에서의 node importance를 capture
- self-attention의 경우 node의 semantic feature를 주로 사용하여 계산되기 때문에, 그러한 정보를 담지 못함
- degree centrality 활용
- 학습가능한 벡터가 노드의 degree에 따라 각 노드에 할당되고, 이것이 input layer의 node feature들에 더해지는 방식
- 경험적인 연구들은 간단한 centrality encoding도 그래프 데이터에의 transformer 모델링에 효과적인 것을 보여줌
연결 중심성(Degree Centrality)
: 한 Node에 연결된 모든 Egde의 갯수(Weighted 그래프일 경우에는 모든 W eight의 합)로
중심성을 평가
- Spatial Encoding
- 목적 : 노드들 사이 structural relation을 capture
- graph-structured data는 이미지나 자연어같은 structured data와는 달리 임베딩 하기위한 canonical grid(표준 격자)가 없음
- 노드들은 non-Euclidean space에 엣지로 연결되어 존재함
- 이를 모델링하기 위해, 각 노드쌍에 대해 spatial realtion을 기반으로한 학습가능한 임베딩을 할당
- Multiple measurements in the literature could be leveraged for modeling spatial relations.
- spatial relation들을 모델링하기 위해
- 일반적으로, 증명을 위해 어떤 두개 노드 사이 shortest path의 거리를 계산
- softmax attention의 bias term으로 encoded
- 그래프의 spatial dependency를 정확히 capture하는데 기여
- 추가적인 spatial information은 edge의 feature(ex. 분자구조에서 두개의 원자사이 연결의 종류)를 포함하기도 함
- new edge encoding method :
- transformer layer에 singnal추가하기 위함
- 각 노드쌍에 대해, 최단 거리에서의 학습가능한 임베딩과 edge feature의 dot product의 평균을 계산해 attention module에 사용
- 이러한 인코딩을 통해 Graphormer는 노드쌍의 관계를 더 잘 표현함
- Strong expressiveness
2. Preliminary
Graph Neural Network (GNN)
- AGGREGATE : 이웃노드의 정보 aggregation
- COMBINE : 노드 representation에 이웃노드로 부터 aggregation한 정보를 융합
- READOUT : 노드 feature를 final representation에 aggregate
Transformer
- Query
- Key
- Value
3. Graphormer
3.1 Structural Encodings in Graphormer
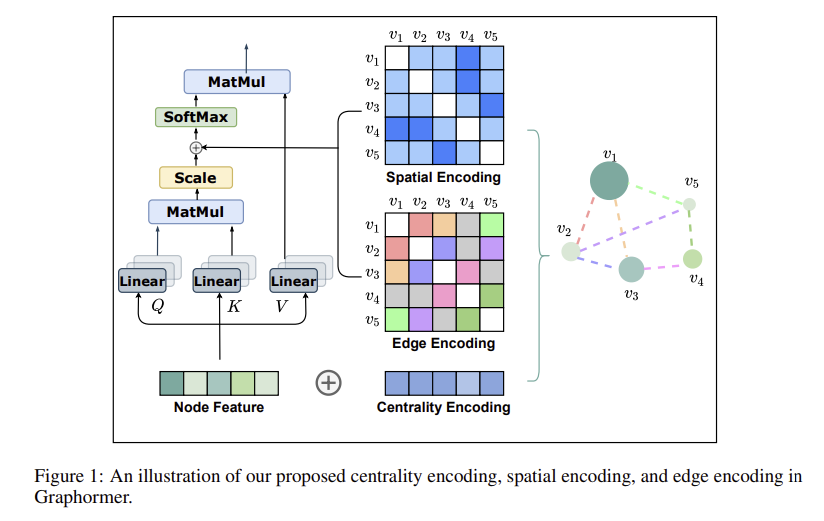
3.1.1 Centrality Encoding
attention distribution은 노드들 사이 correlation을 기반으로 계산됨
node centrality는 노드의 중요성을 의미하는데, 그래프 이해의 중요한 정보
현재의 attention계산 방법은 그러한 정보를 무시하고있음
Degree centrality
- indegree와 outdegree에 따른 2개의 실수 임베딩 벡터를 할당
- 각 노드에 대한 centrality encoding을 node feature와 합침
$h_i^{(0)} = x_i + z^−_{deg^−(vi)} + z^+ _{deg ^+ (vi)}$
$deg^−(vi), deg^+(vi)$ : indegree, outdegree 학습가능한 임베딩 벡터
- 무방향 그래프에 대해서는 unified to $deg(v_i)$
- centrality encoding을 input으로 사용함으로써, softmax attention은 쿼리와 키에서 노드 importance signal을 잡아낼 수 있음
- 따라서 모델은 attention mechanism을 통해 sematic correlation과 node importance를 모두 포함
3.1.2 Spatial Encoding
- Transformer의 장점 중 하나인 global receptive field
- Transformer의 byproduct problem : 모델이 explicit하게 position을 구분하고 encoding함 (ex.positional embedding)
- 그래프에서는 이러한 sequence가 필요없음 → node가 sequence로 정렬되어있지 않음
- instead, multi-dimensional spatial space에 존재하며, edge들로 연결됨
- 그래프에서는 이러한 sequence가 필요없음 → node가 sequence로 정렬되어있지 않음
structural information을 encoding하기 위한 spatial encoding방법을 제안
- spatial encoding : $\phi(vi_i,v_j) : V \times V \rightarrow \mathbb R$
- Graph $G$에서 $v_i, v_j$사이 spatial relation
- $\phi(vi_i,v_j)$는 노드들 사이 connectivity로 정의될 수 있음
- distance of shortest path(SPD)
- 연결안된경우 -1
- 각 output값에 학습가능한 scalar값을 부여해 self-attention 모듈의 bias term 역할을 하게됨
- $A_{ij}$ : Query-Key matrix A의 $(i,j)$th element
- $b_{\phi(v_i,v_j)}$ : $\phi(vi_i,v_j)$로 인덱싱된 학습가능한 scalar 값
- 값은 모든 레이어에서 공유
- Graph $G$에서 $v_i, v_j$사이 spatial relation
$A_{ij} = \frac{(h_iW_Q)(h_jW_k)^T}{\sqrt{d}} + b_{\phi(v_i,v_j)}$
제안된 방법론의 장점
- receptive field가 이웃 노드들로 제한되는 conventional GNN과 비교했을 때 transformer layer는 그래프 내의 모든 다른 노드들의 attend하며 global information을 제공
- $b_{\phi(v_i,v_j)}$을 적용함으로써, transformer layer의 각 노드는 그래프의 구조적 정보(structural information)에 따라서 adaptively attend
- ex. $b_{\phi(v_i,v_j)}$가 $\phi(vi_i,v_j)$에 따라 감소함수로 학습되었을 경우 → 모델은 가까운 노드를 더 attend하고, 멀리있는 노드는 상대적으로 덜 attend하게됨
3.1.3 Edge Encoding in the Attention
edge또한 구조적 특성을 가지는 경우
- ex. molecular graph, 원자쌍 사이 연결이 특정 type을 가지기도 함
- Traditional methods for edge encoding
- edge features가 연관된 nodes’ features에 더해짐
- 각 노드에 대해 연관된 edges’ features는 aggregation단계에서 node features와 함께 사용됨
- 연관된 노드와의 edge 정보만 전파 → 전체 그래프에서는 좋지 않을 수 있음
⇒ 노드간 shortest path를 찾고, path를 따라 edge feature와 학습가능한 임베딩을 dot product하여 평균내는 방식
- attention mechanism은 각 node pair $(v_i, v_j)$d에 대해 correlation을 계산해야함
- $v_i$에서 $v_j$로 가는 shortest path $SP_{ij} = (e_1,e_2, ..., e_N)$
- spatial encoding처럼 bias term을 통해 추가됨
$A_{ij} = \frac{(h_iW_Q)(h_jW_k)^T}{\sqrt{d}} + b_{\phi(v_i,v_j)}+c_{ij}, ~~\text{where} ~c_{ij} = \frac{1}{N}\sum_{n=1}^{N}x_{e_n}(w_n^E)^T$
- $x_{e_n}$ : $SP_{ij}$ 에서 $n$번째 edge $e_n$의 feature
- $w_n^R \in \mathbb R^{d_E}$ : $n$번째 weight embedding
- $d_E$ : edge feature의 dimensionality
3.2 Implementation Details of Graphormer
Graphormer Layer
Basic Transformer의 encoder에
- Multi-head self-attnetion(MHA)와 Feed-foward block(FFN)이전에 Layer Normalization(LN) 추가
- for effective optimization
- FFN sub-layer에 대해서는 input, output, inner-layer를 $d$ dimension으로 통일
$h^{
′
(l)} = MHA(LN(h^{
(l−1)})) + h^{
(l−1)}$
$h^{
(l)} = FFN(LN(h^{
′
(l)}
)) + h^{
′
(l)}$
Special Node
[VNode]
- 그래프 내의 모든 노드와 각각 연결
- Aggregate-Combine 단계를 통해 그래프 전체의 representation을 학습하게됨
reset all spatial encodings for $b_{ϕ([VNode],v_j)}$ and $b_{ϕ(v_i,[VNode])}$ to a distinct learnable scalar
3.3 How Powerful is Graphormer?
Fact 1. By choosing proper weights and distance function ϕ, the Graphormer layer can represent AGGREGATE and COMBINE steps of popular GNN models such as GIN, GCN, GraphSAGE.
- spatial encoding → self attention이 이웃 노드들과 노드를 구분하게 함
- node degree
Fact 2. By choosing proper weights, every node representation of the output of a Graphormer layer without additional encodings can represent MEAN READOUT functions.
- simulate graph-level READOUT operation to aggregate information from the whole graph
- No over-smoothing
4. Experiments
4.1 OGB Large-Scale Challenge
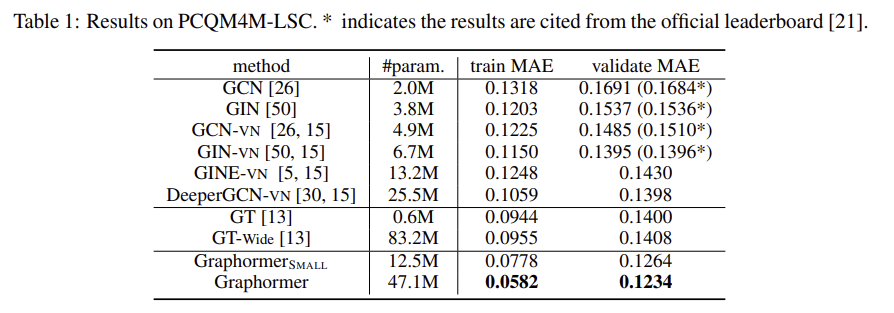
4.2 Graph Representation
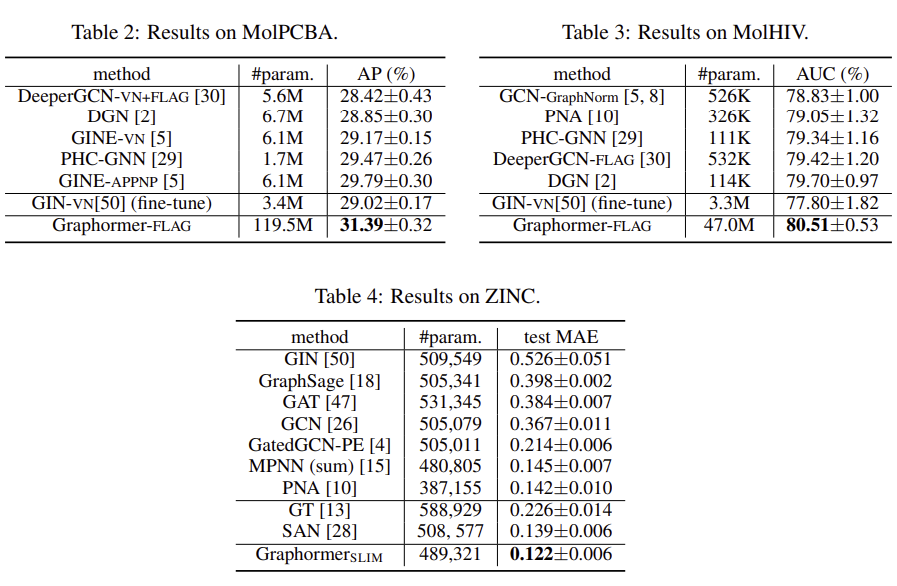
6. Conclusion
- graph structural encodings
- Centrality Encoding
- Centrality Encoding
- Edge Encoding
- works well on wide range of popular benchmark datasets
- challange
- quadratic complexity of the self-attention module restricts Graphormer’s application on large graphs
