| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | ||
| 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 13 | 14 | 15 | 16 | 17 | 18 | 19 |
| 20 | 21 | 22 | 23 | 24 | 25 | 26 |
| 27 | 28 | 29 | 30 |
- YAI 8기
- rl
- PytorchZeroToAll
- YAI 11기
- 자연어처리
- YAI 9기
- 연세대학교 인공지능학회
- VIT
- Perception 강의
- 강화학습
- 컴퓨터 비전
- RCNN
- NLP
- CS231n
- cl
- NLP #자연어 처리 #CS224N #연세대학교 인공지능학회
- Fast RCNN
- nerf
- GaN
- 컴퓨터비전
- Faster RCNN
- Googlenet
- transformer
- GAN #StyleCLIP #YAI 11기 #연세대학교 인공지능학회
- CNN
- YAI
- YAI 10기
- CS224N
- 3D
- cv
- Today
- Total
연세대 인공지능학회 YAI
[논문 리뷰] Playing Atari with Deep Reinforcement Learning 본문
Playing Atari with Deep Reinforcement Learning
https://arxiv.org/abs/1312.5602
*YAI 10기 최서연
님이 작성한 글입니다.
1. Introduction
기존의 RL algorithm들은 모두 직접 사람이 만든 linear value function이나 policy representation들을 사용했었다. 하지만 비전이나 자연어같은 분야들에서 neural network들을 사용한 알고리즘이 굉장히 성공을 거두며 RL에도 비슷한 종류의 net을 사용할 수 있는 지가 논의의 중심이 되었다.
Reinforcement Learning에는 항상 풀지 못하는 숙제들이 있다.
- Sparse & Delayed Rewards
input과 target값이 바로 주어지는 supervised learning과는 다르게 RL은 action에 따른 reward값이 굉장히 sparse하게, 그리고 굉장히 delay되어서 주어진다. - High correlated datas
모든 deep learning algorithm들은 data들이 independent하다는 가정 하에 이루어졌는데 RL은 연속된 seuquence에서 나오는 data다보니 모두 dependent하게 연관되어있다. - Non-stationdary data distributions
마찬가지로 RL은 연속된 sequence에 따라서 학습되고 data가 나오다보니, data들이 같은 policy 아래에서 학습된 것이 아닌 매번 달라지는 policy에 따라 학습된 data들이다.
해당 논문은 이런 문제들을 아래의 방법을 사용해서 해결한다.
- Convolutional neural network
Q-learning mechanism + stochastic gradient descent - Experience replay mechanism
이전의 transition들에서 랜덤하게 샘플링해 데이터를 학습한다. - 사람이 만든 function/feature들을 사용하지 않고 오로지 video input을 통해서만 학습한다.
- network나 hyperparameter들이 변하지 않고 일정하다.
이 새로운 algorithm들을 통해 Atari 2600 Games 6개를 성공적으로 학습시켰다.
2. Background
Basic Schemetics
매 time step t마다
- Agent는 game action A에서 1가지 선택
- Atari emulator(= envronment E )가 action을 기반으로 게임을 업데이트
- Agent는 현재 게임 스크린의 image (xt∈Rd)를 pixel값으로 관측게임 스코어에 따른 reward r_t
- State representation: sequence st=x1, a1, ⋯, at−1, xt
agent는 전체의 게임이 아닌 현재 스크린에 비춰지는 화면만 관측하므로 현재 시점까지의 image xt와 action at−1까지를 포함한 sequence를 state로 생각한다. - Terminates at time step T
→ finite MDP라 가정할 수 있게 된다. - Theory
- Future discounted reward: Rt=∑Tt′=tγt′−trt′
- Optimal state-action value function: Q∗(s,a)=maxπE[Rt|st=s,at=a,π]
- Bellman equation: Q∗(s,a)=Es′∼E[r + γmaxa′Q∗(s′,a′)|s,a]
이론적으로는 Bellman equation을 이용해 value iteration을 통해 optimal한 Q를 구하는 것이 맞다.
Qi+1(s,a)=E[r + γmaxa′Qi(s′,a′)|s,a]
하지만 실제로는 이 방법을 사용하면 다른 sequence마다 Q가 다르게 계산되기 때문에 모든 상황에 generalize되기 어렵다. 따라서 실제로는 function approximator를 사용한다.
- Q-network
논문에서는 weight θ의 neural network function approximator를 사용해 Q를 estimate한다.
이 Q-network는 아래의 loss function를 매 iteration마다 minimize해가며 train시킨다.
Li(θi)=Es,a∼ρ(⋅)[(yi − Q(s,a;θi))2]
- i번째 iteration에서의 target : yi=Es′∼E[r + γmaxa′Q(s′,a′;θi−1)|s,a]
- behaviour distribution: ρ(s,a), sequence s와 action a의 확률분포
→ 이전 i-1 iteration에서 최적의 Q라고 생각하는 target yi와 i번째 iteration의 Q와의 squared error!

Optimization은 stochastic gradient descent를 이용해서 한다.
이 방법은…
- Model-free: emulator에서 나오는 sample들을 직접적으로 사용
- Off-policy: ϵ-greedy stragey 사용
3. Deep Reinforcement Learning
DQN Algorithm

- Experience Replay
매 time step의 et=(st, at, rt, st+1)를 dataset D=e1, ⋯, eN에 저장한다.
이후 update를 할 때 이 dataset에서 랜덤하게 experience를 샘플링해서 사용한다.
실제로는 전체 experience를 저장하지 않고 마지막 N개의 experience만 사용한다. - Fixed length representation function ϕ
위의 이론에서는 sequence s를 모두 사용하는게 좋다고 하지만 neural net에 모든 sequence를 넣어주기에는 길이가 너무 길다. 따라서 sequenc
를 짧게 preprocessing해주는 함수를 사용한다.
DQN의 장점
- experience가 여러 update에 사용되기 때문에 data efficiency가 더 높다.
- sample들을 랜덤하게 사용하기 때문에 correlation이 없어진다.
- 이전의 state들을 랜덤하기 사용하기 때문에 behaviour distribution이 평균화된다.
DQN의 한계
- Memory buffer D안에서 중요한 experience들을 구분하지 못한다.
- Memory size가 한정되다보니 최근의 experience들로 덮어 씌워진다.
3.1 Preprocessing and Model Architecture
Preprocessing images

- Function ϕ가 마지막 4개의 frame만을 사용하도록 한다.
### Model Architecture
Q를 parameterize하기 위해 기존의 방법들은 history와 action을 모두 neural net에 input으로 사용했다. 하지만 이런 방식의 경우 각각의 forward pass가 요구되었기 때문에 DQN은 action은 다른 output unit을 만들어주고 state representation(= history)만 input으로 넣어주었다. 이런 방식을 사용하면 1개의 forward pass만 사용해서 훨씬 수월하다.
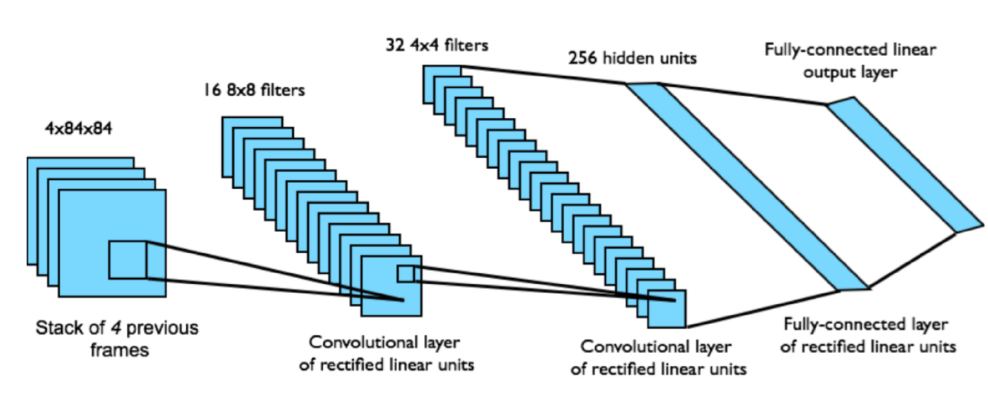
4. Experiments
7개의 Atari games: Beam Rider, Breakout, Enduro, Pong, Q*bert, Seaquest, Space Invaders
DQN이 robust하다는 것을 보이기 위해 모두 같은 architecture를 사용했다.
- Game마다 다른 특성들을 적용하지 않았다.
- Reward function의 경우, 게임들마다 score 체제가 너무 다르기 때문에 긍정적 reward는 모두 +1, 부정적 reward는 모두 -1을 부여했다.
- Game play시간을 늘리고 computation양을 줄이기 위해 frame-skipping 사용
모든 게임에서 k=4, Space Invaders만 k=3
- RMSProp, minibatch of 32
- ϵ-greedy with ϵ linear 1 to 0.1 until 1M frames, and fixed 0.1 after
- Replay memory of last 1M frames
- Trained total 10M frames
4.1 Training and Stability
강화학습에서 training 도중의 progress를 evaluate하는 방법으로 2가지를 제시한다.
- Average Total Reward
한 episode 또는 여러 게임들에서 total reward를 average한 값을 사용하는 것이다.
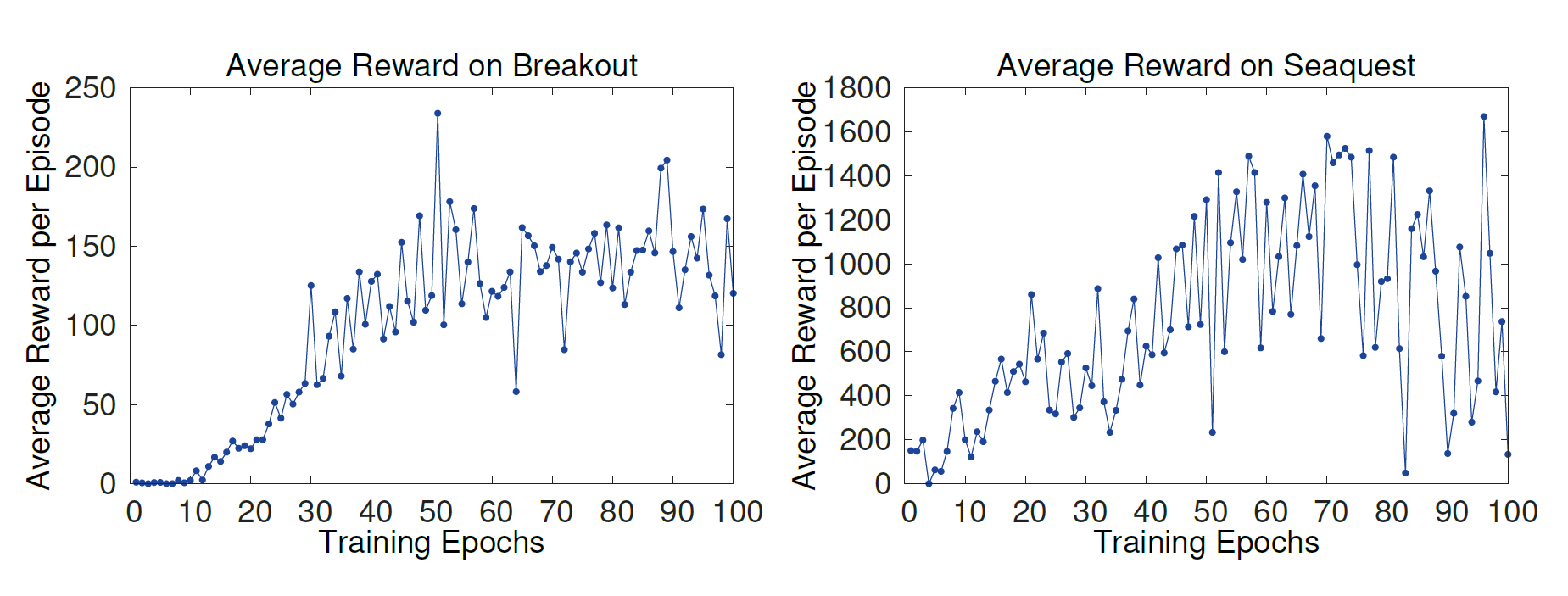
하지만 위의 사진과 같이 굉장히 noisy한 모습을 보인다. Policy weight들의 작은 변화에도 방문하는 state들이 굉장히 달라지기 때문이다.
- Average maximum predicted action-value function Q
매 epoch마다 training이 시작하기 전에 random으로 여러 policy를 생성해서 maximum predicted Q값을 average한 값을 사용한다.
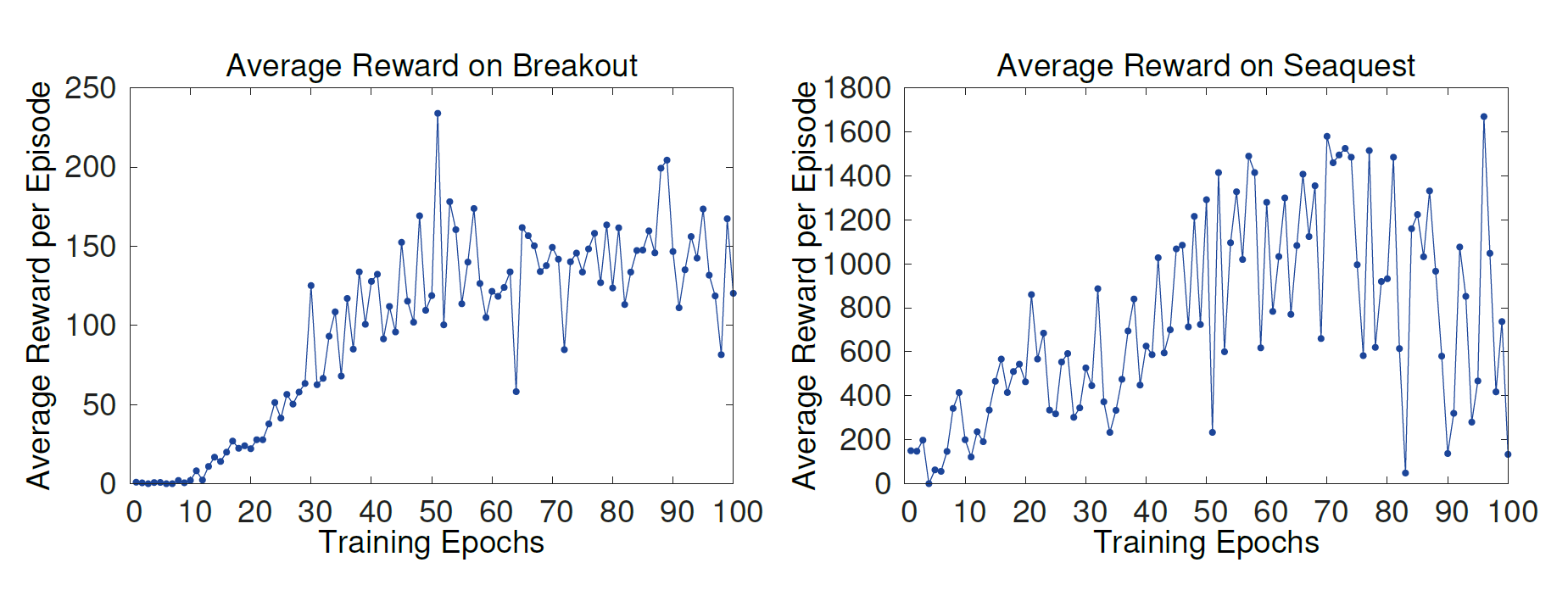
Average total reward보다 훨씬 부드러운 모습을 보인다. 또한 이 방법이 이론적으로는 증명된 바가 없으나 논문에서 실험했을 때 한번 diverge 한 적이 없어 믿을 만한 방법이라고 한다.
4.2 Visualizing the Value Function
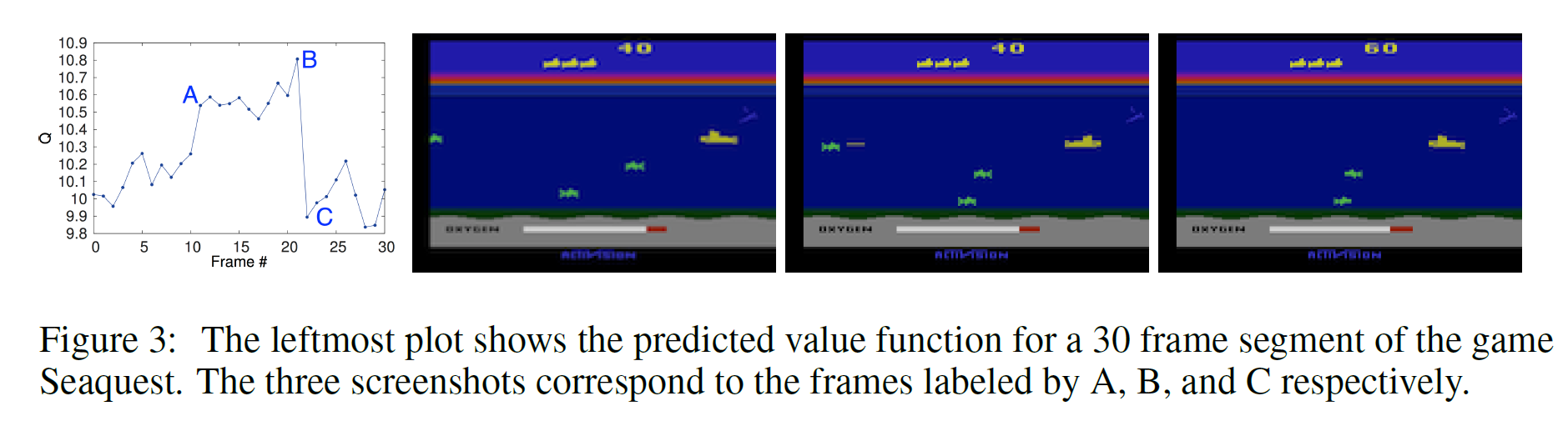
실제 게임해서 적이 나타나고 격침시킬 때 value function값이 커지는 것을 볼 수 있다.
4.3 Main Evaluation
Evaluation을 위해서 train된 DQN net에 ϵ이 0.05인 ϵ-greedy policy를 사용했다.

위의 표는 average total reward값들을 algorithm별로 비교한 표이다.
DQN이 다른 알고리즘들에 비해 월등한 성적을 보이는 것을 볼 수 있다.
5. Conclusion
Atari의 7개의 game들에 DQN을 적용해본 결과, 알고리즘이 성공적인 것을 알 수 있다.
'강화학습 : RL' 카테고리의 다른 글
| [논문 리뷰] Playing Atari with Deep Reinforcement Learning (0) | 2023.03.04 |
|---|---|
| [논문 리뷰] Asynchronous Methods for Deep Reinforcement Learning (1) | 2023.01.14 |


